Marty McFly realizes he is running out of time to submit his solution

Did you know that our Physics Challenge problem contest thingy is still up and going? It is! The contest will be open until the end of the day this Friday, November 4th. And, unlike last time, the winning solution will be chosen and posted by the end of the weekend. So even if you don't submit your own solution (though you totally should), check back here Monday morning for the winning entry. Why should you submit a solution to our problem? Lots of reasons! The top ten reasons as decided by a random sample of me are given below the break. Top Ten Reasons to Submit a Solution: 1) You will win super-awesome prizes! What kinds of prizes? Well how does a greeting card with kittens on the front and a collection of encouraging haikus from the entire Virtuosi staff written inside sound? It sounds awesome, awesome to the max. 2) You get to show off your totally rad physics skills! 3) You can put it on your resume/cv! The semi-annual Virtuosi Physics Challenge problem winners are held to the same esteem as Fields Medalists and Nobel Prize winners! 4) You will earn the respect and admiration of your peers! Winners of this contest develop an aura that all other people can see, fear, and respect. 5) You will become stronger, faster, and more productive than ever before! This is a scientifically proven fact perhaps. 6) You may gain the ability to talk to animals! Have you ever wanted to discuss espionage-related topics with a platypus (perhaps this platypus)? Of course you have! Winners can! 7) You will be in Presidential company! Did you know William Henry Harrison won the very first Virtuosi physics challenge contest shortly before becoming the ninth President of the United States? Yep! Tippecanoe and so can you! 8) Alemi will salute in your general direction. No questions asked. 9) You will give me work to do on the weekend! This will give my dull and uninteresting life a small glimmer of meaning! Hooray! 10) There's like a 50% chance that you will get three wishes from a magical genie named David Bowie (no relation). Seriously. Like 50%. That should get you properly motivated! So check out the Challenge Problem website and when you have a solution, send it to our email address (given up in the sidebar). Good luck!

Recently I set out to hold a Battleship programming tournament here among some of the undergraduates. Naturally, I myself wanted to win. So, I got to thinking about the game, and developed what I like to call "the linear theory of battleship". A demonstration of the fruits of my efforts can be found here. Below, my aim is to guide you through how I developed this theory, as an exercise in using physics to solve an interesting unknown problem. This is one of the things I really love about physics, the fact that obtaining an education in physics is essentially an education in reasoning and thinking through complicated problems, along with an honestly short list of tips and tricks that have proven successful for tackling a wide range of problems. So, how do we develop the linear theory of battleship? First we need to quantify what we know, and what we want to know.

The Goal

So, how does one win Battleship? Since the game is about sinking your opponents ships before they can sink yours, it would seem that a good strategy would be to try to maximize your probability of getting a hit every turn. Or, if we knew the probabilities of there being a hit on every square, we could guess each square with that probability, to keep things a little random. So, let's try to represent what we are after. We are after a whole set of numbers $$ P_{i,\alpha} $$ where i ranges from 0 to 99 and denotes a particular square on the board, and alpha can take the values C,B,S,D,P for carrier, battleship, submarine, destroyer, and patrol boat respectively. This matrix should tell us the probability of there being the given ship on the given square. E.g. $$ P_{53,B} $$ would be the probability of there being a battleship on the 53rd square. If we had such a matrix, we could figure out the probability of there being at hit on every square by summing over all of the ships we have left, i.e. $$ P_i = \sum_{\text{ships left}} P_{i, \alpha } $$

The Background

Alright, we seem to have a goal in mind, now we need to quantify what we have to work with. Minimally, we should try to measure the probabilities for the ships to be on each square given a random board configuration. Let's codify that information in another matrix $$ B_{i,\alpha} $$ where B stands for 'background', i runs from 0 to 99, and alpha is either C,B,S,D, or P again, and stands for a ship. This matrix should tell us the probability of a particular ship being on a particular spot on the board assuming our opponent generated a completely random board. This is something we can measure. In fact, I wrote a little code to generate random Battleship boards, and counted where each of the ships appeared. I did this billions of times to get good statistics, and what I ended up with is a little interesting. You can see the results for yourself over at my results exploration page by changing the radio buttons for the ship you are interested in, but I have some screen caps below. Click on any of them to embiggen.

All

First of all, lets look at the sum of all of the ship probabilities, so that we have the probability of getting a hit on any square for any ship given a random board configuration, or in our new parlance $$ B_i = \sum_{\alpha={C,B,S,D,P} } B_{i,\alpha} $$ The results:

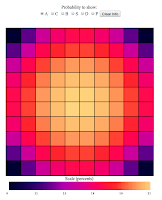
shouldn't be too surprising. Notice first that we can see that my statistics are fairly good, because our probabilities look more or less smooth, as they ought to be, and show nice left/right up/down symmetry, which it ought to have. But as you'll notice, on the whole there is greater probability to get a hit near the center of the board than near the edges, an especially low probability of getting a hit in the corners. Why is that? Well, there are a lot more ways to lay down a ship such that there is a hit in a center square than there are ways to lay a ship so that it gives a hit in a corner. In fact, for a particular ship there are only two ways to lay it so that it registers a hit in the corner. But, for a particular square in the center, for the Carrier for example there are 5 different ways to lay it horizontally to register a hit, and 5 ways to lay it vertically, or 10 ways total. Neat. We see entropy in action.

Carrier

Next let's look just at the Carrier:

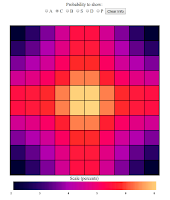
Woah. This time the center is very heavily favored versus the edges. This reflects the fact that the Carrier is a large ship, occupying 5 spaces, basically no matter how you lay it, it is going to have a part that lies near the center.

Battleship

Now for the Battleship:

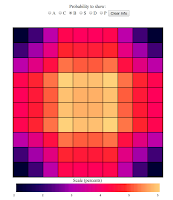
This is interesting. This time, the most probable squares are not the center ones, but the not quite center ones. Why is that? Well, we saw that for the Carrier, the probability of finding it in the center was very large, and so respectfully, our battleship cannot be in the center as often, as a lot of the time it would collide with the Carrier. Now, this is not because I lay down the Carrier first, my board generation algorithm assigns all of the boards at once, and just weeds out invalid ones, this is a real entropic effect. So here we begin to see some interesting Ship-Ship interactions in our probability distributions. But notice again that on the whole, the battleship should also be found near the center as it is also a large ship.

Sub / Destroyer

Next let's look at the sub / destroyer. First thing to note is that our plot should be the same for both of these ships as they are both the same length.

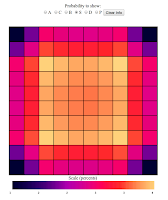
Here we see an even more pronounced effect near the center. The Subs and Destroyers are 'pushed' out of the center because the Carriers and Battleships like to be there. This is a sort of entropic repulsion.

Patrol Boat

Finally, let's look at the patrol boat:

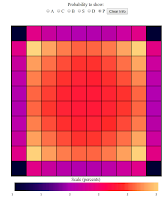
The patrol boat is a tiny ship. At only two squares long, it can fit in just about anywhere, and so we see it being strongly affected by the affection the other ships have for the center. Neat stuff. So, we've experimentally measured where we are likely to find all of the battleship ships if we have a completely random board configuration. Already we could use this to make our game play a little more effective, but I think we can do better.

The Info

In fact, as a game of battleship unfolds, we learn a good deal of information about the board. In fact on every turn we get a great deal of information about a particular spot on the board, our guess. Can we incorporate this information into our theory of battleship? Of course we can, but first we need to come up with a good way to represent this information. I suggest we invent another matrix! Let's call this one $$ I_{j,\beta} $$ Where I is for 'information', j goes from 0 to 99 and beta marks the kind of information we have about a square, let's let it take the values M,H,C,B,S,D,P, where M means a miss, H means a hit, but we don't know which ship, and CBSDP mark a particular ship hit, which we would know once we sink a ship. This matrix will be a binary one, where for any particular value of j, the elements will all be 0 or 1, with only one 1 sitting at the spot marking our information about the square, if we have any. That was confusing. What do I mean? Well, let's say its the start of the game and we don't know a darn thing about spot 34 on the board, then I would set $$ I_{34,M}=I_{34,H}=I_{34,C}=I_{34,B}=I_{34,S}=I_{34,D}=I_{34,P}=0 $$ that is, all of the columns are zero because we don't have any information. Now let's say we guess spot 34 and are told we missed, now that row of our matrix would be $$ I_{34,M} = 1 \quad I_{34,H}=I_{34,C}=I_{34,B}=I_{34,S}=I_{34,D}=I_{34,P}=0 $$ so that we put a 1 in the column we know is right, instead, if we were told it was a hit, but don't know which ship it was: $$ I_{34,H} = 1 \quad I_{34,M}=I_{34,C}=I_{34,B}=I_{34,S}=I_{34,D}=I_{34,P}=0 $$ and finally, lets say a few turns later we sink our opponents sub, and we know that spot 34 was one of the spots the sub occupied, we would set: $$ I_{34,S} = 1 \quad I_{34,M}=I_{34,H}=I_{34,C}=I_{34,B}=I_{34,D}=I_{34,P}=0 $$ This may seem like a silly way to codify the information, but I promise it will pay off. As far as my Battleship Data Explorer goes, you don't have to worry about all this nonsense, instead you can just click on squares to set their information content. Note: shift-clicking will let you cycle through the particular ships, if you just regular click it will let you shuffle between no information, hit, and miss.

The Theory

Alright if we decide to go with my silly way of codifying the information, at this point we have two pieces of data, $$ B_{i,\alpha} $$ our background probability matrix, and $$ I_{j,\beta} $$ our information matrix, where what we want is $$ P_{i,\alpha} $$ the probability matrix. Here is where the linear part comes in. Why don't we adopt the time honored tradition in science of saying that the relationship between all of these things is just a linear one? In matrix language that means we will choose our theory to be $$ P_{i,\alpha} = B_{i,\alpha} + \sum_{j=[0,..,99],\beta={M,H,C,B,S,D,P}} W_{i,\alpha,j,\beta} I_{j,\beta} $$ Whoa! What the heck is that!? Well, that is my linear theory of battleship. What the equation is trying to say is that I will try to predict the probability of a particular ship being in a particular square by (1) noting the background probability of that being true, and (2) adding up all of the information I have, weighting it by the appropriate factor. So here, P is our probability matrix, B is our background info matrix, I is our information matrix, and W is our weight matrix, which is supposed to apply the appropriate weights. That W guy seems like quite the monster. It has four indexes! It does, so let's try to walk through what they all mean. Here: $$ W_{i,\alpha,j,\beta} $$ is supposed to tell us: "the extra probability of there being ship alpha at location i, given the fact that we have the situation beta going on at location j" Read that sentence a few times. I'm sorry its confusing, but it is the best way I could come up with explaining W in english. Perhaps a visual would help. Behold the following: (click to embiggen)

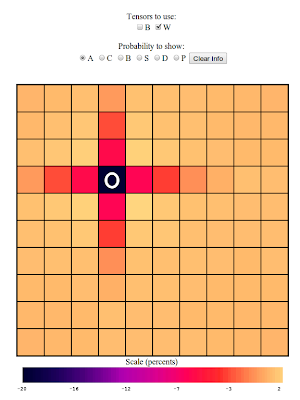
That is a picture of $$ W_{i,C,33,M} $$ that is, that is a picture of the extra probabilities for each square (i is all of them), of there being a carrier, (alpha=C) given that we got a miss (beta=M) on square 33, (j=33). You'll notice that the fact that we saw a miss affects some of the squares nearby. In fact, knowing that there was a miss on square 33 means that the probability that the carrier will be found on the adjacent squares is a little lower (notice on the scale that the nearby values are negative), because there are now fewer ways the carrier could be on those squares without it overlapping over into square 33. Let's try another:

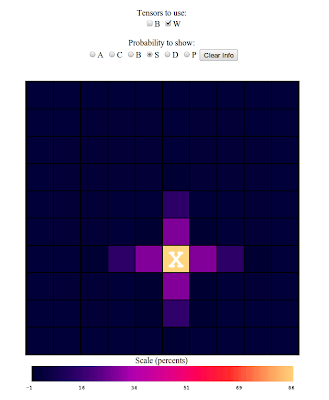
That is a picture of $$ W_{i,S,65,H} $$ that is, it's showing the extra probability of there being a submarine (alpha=S), at each square (i is all of them, since its a picture with 100 squares), given that we registered a hit (beta=H) on square 65 (j=65). Here you'll notice that since we marked a hit on square 65, it is very likely that we will also get hits on the squares just next to this one, as we could have suspected. In the end, by assuming our theory has this linear form, the benefit we gain is that by doing the same sort of simulations I did to generate the background information, I can back out what the proper values should be for this W matrix. By doing billions and billions of simulations, I can ask, for any particular set of information, I, what the probabilities are P, and solve for W. Given that the problem is linear, this solving step is particularly easy for me to do.

The Results

In the end, this is exactly what I did. I had my computer create billions of different battleship boards, and figure out what the proper values of B and W should be for every square of the matrix. I put all of those results together in a way that I hope is easy to explore up at the Fancy Battleship Results Page, where you are free to explore all of the results yourself. In fact, the way it's set up, you can even use the Superduper Results Page as a sort of Battleship Cheat Sheet. Have it open while you play a game of battleship, and it will show you the probabilities associated with all of the squares, helping you make your next guess. I've used the page while playing a few games of battleship online, and have had some success, winning 9 of the 10 games I played against the computer player. Of course, this linear theory isn't everything...

Why Linear isn't everything

But at the end of the day, we've made a pretty glaring assumption about the game of battleship, namely that all of the information on the board adds in a linear way. Another way to say that is that in our theory of battleship, we have a principle of superposition. Another way to say that is that in this theory, what you think is happening in a particular square is just the sum of the results from all of the squares, independent of one another. 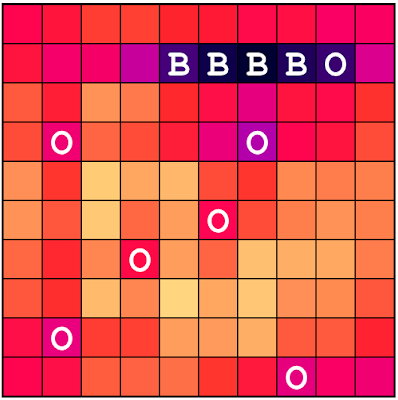Another way to say that is to show it with another picture. Consider the following:

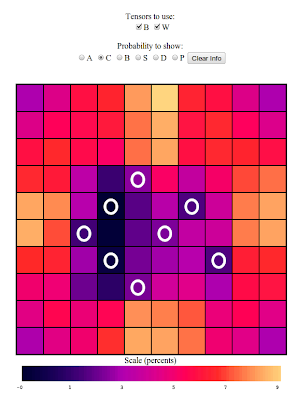
Here, I've specified a bunch of misses, and am asking for the probability of there being a Carrier on all of the positions of the board. If you look in the center of that cluster of misses, especially in the inner left of the bunch, you'll see that the linear theory tells me that there is a small but finite chance that the Carrier is located on those squares. But if you stop to look at the board a little bit, you'll notice that I've arranged the misses such that there is a large swatch of squares in the center of the cluster where the Carrier is strictly forbidden. There is no way it can fit such that it touches a lot of those central squares. This is an example of the failure of the linear model. All the linear model knows is that in the spots nearby misses there is a lower probability of the ship being there, but what it doesn't know to do is look at the arrangement of misses and check to see whether there is any possible way the ship can fit. This is a nonlinear effect, involving information at more than one square at a time. It is these kinds of effects that this theory will miss, but as you'll notice, it still does pretty well. Even though it reports a finite positive probability of the Carrier being inside the cluster, the value it reports is a very small one, about 1 percent at most. So the linear theory will have corrections at the 1 percent level or so, but that's pretty good if you ask me.

Summary

And so it is. I've tried to develop a linear theory for the game Battleship, and display the results in a Handy Dandy Data Explorer. I encourage you to play around with the website, use it to win games of Battleship, and in the comments, point out interesting effects, things you think I've missed, or ideas for how to come up with linear theories of other things.

Doc Brown didn't have a time-travel backup plan.

In light of the incredible success of our last Physics Challenge Problem (we received several responses), we here at the Virtuosi have decided to reinstate what was nominally a "monthly" contest. In addition to a brand-spankin'-new problem (with "prizes", see [1]), we have also tried to make a nice collaborative environment for discussing interesting physics problems and posting your own solutions. So I will discuss our new problem and then I'll throw it over to Alemi to discuss the goal of our new Physics Challenge webpage. Our last challenge problem (here, with winning solutions) was deemed a bit "unrealistic" by many because it assumes that you were shipwrecked on a desert island with a CRC handbook! What a ridiculous situation! Fear not, dear readers, we have heard your complaints and have adjusted accordingly. Our new problem relies on a far less ridiculous assumption. Assume you have created a time machine out of a DeLorean [2]. You are sure it will send you back in time and, causality-be-damned, you are ready to give it a test drive. But you are less confident in the machine's ability to take you exactly when you want. Additionally, the positive tachyonic chrono-coupler is a bit finicky - meaning, of course, that there is a non-negligible chance that once you go back in time, you may never be able to come Back to the Present. Thus, there is a chance that your time machine will have worked but no one will ever know! As an unabashed narcissist, you find this totally unacceptable! But first and foremost, you are a scientist. As a scientist, your challenge is to design a strategy that would allow you to convince your present-day scientific peers that you did travel back in the time even if you are stuck in the past. What could you build/make/leave in the past that would be most likely to convince modern scientists that it had to be from a time-traveler and not just some hoaxer? How long would your strategy be effective? Would it work if you were stuck ten thousand years in the past? What about a million years in the past? What about 100 million? Though this is an inherently silly problem, we feel that the idea behind it is a very interesting one. What could one motivated person do/build/make that would survive a long time into the future? Also, the winning solution will be submitted as a policy White Paper for all future time-travelers. So that's the new problem. You can find the "official" posting here. I now cede the floor and my remaining time to the gentleman from Wisconsin.

A sense of community...

So, we've had this blog going for a while now, and we get a decent number of comments on our posts, but felt as though something has been lacking. A certain sense of community. Over the past year, we've done some neat things here, and now it's your turn. Step right up, because we've just launched a google groups: TheVirtuosi where we hope people from all corners of the globe will gather to discuss their kooky physics projects. Have you recently explored the physics of cats? Launch a discussion. Do you have an idea but need some help investigating it? Create a discussion and query us and all of our fantastic readers. Have an idea for a blog post you want to see? Let us know. Want to take a stab at solving one of the newly minted Physics Challenge problems in public? Go for it! I know the site is sparse now, but we'd really like to build a little bit of a community here, so please, post away. You all have already bookmarked it I'm sure, but a permanent link has been added to the top of the sidebar as well. That is all. [1] These "prizes" will no longer be as exciting as the CRC from last time, for several reasons. First of all, we are all poor grad students and have no money. Secondly, the winners from last time lived as far away from us as physically possible and it's expensive to ship heavy things. So what can you expect to win? Well, you could win a "certificate of accomplishment" which would just be drawn in crayon by one of this. But it will be made with love! Or you could win a floppy disk with a recording of my very own version of the Jurassic Park theme. The surprise is part of the fun (I'm told). [2] Quoth the most famous chrononaut of our time, Dr. Emmett Brown: "The way I see it, if you're gonna build a time machine into a car, why not do it with some style?"

So, I recently read An Introduction to Information Theory: Symbols, Signals and Noise. It is a very nice popular introduction to Information Theory, a modern scientific pursuit to quantify information started by Claude Shannon in 1948. This got me thinking. Increasingly, people try to hold conversations on Twitter, where posts are limited to 140 characters. Just how much information could you convey in 140 characters? After some coding and investigation, I created this, an experimental twitter English compression algorithm capable of compressing around 140 words into 140 characters. So, what's the story? Warning: It's a bit of a story, the juicy bits are at the end. UPDATE: Tomo in the comments below made a chrome extension for the algorithm

Entropy

Ultimately, we need some way to assess how much information is contained in a signal. What does it mean for a signal to contain information anyway? Is 'this is a test of twitter compression.' more meaningful than '歒堙丁顜善咮旮呂'? The first is understandable by any english speaker, and requires 38 characters. You might think the second is meaningful to a speaker of chinese, but I'm fairly certain it is gibberish, and takes 8 characters. But, the thing is if you put those 8 characters into the bottom form here, you'll recover the first. So, in some sense to the messages are equivalent. They contain the same amount of information. Shannon tried to quantify how we could estimate just how much information any message contains. Of course it would be very hard to try to track down every intelligent being in the universe and ask them if any particular message had any meaning to them. Instead, Shannon reserved himself to trying to quantify how much information was contained in a message produced by a random source. In this regard, the question of how much information a message contains becomes a more tractable question: How unlike is a particular message from all other messages produced by the same random source? This question might sound a little familiar. It is similar to a question that comes up a lot in Statistical Physics, where we are interested in just how unlike a particular configuration of a system is from all possible configurations of a system. In Statistical physics, the quantity that helps us answer questions like this is the Entropy, where the entropy is defined as $$ S = -\sum_i p_i \log p_i $$ where p_i stands for the probability of a particular configuration, and we are supposed to sum over all possible configurations of the system. Similarly, for our random message source, we can define the entropy in exactly the same way, but for convenience, let's replace the logarithm with the logarithm base 2. $$ S = -\sum_i p_i \log_2 p_i $$ At this point, the Shannon Entropy, or Information Entropy takes on a real quantitative meaning. It reflects how many bits of information the message source produces per character. The result of all of this aligns quite well with intuition. If we have a source that outputs two symbols 0 or 1 randomly, each with probability 1/2. The shannon entropy comes out to be 1, meaning each of the symbols of our source is worth one bit, which we already new. If instead of two symbols, our source can output 16 symbols, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F say, the shannon entropy comes out to be 4 bits per symbol, which again we should have suspected since with four bits we can count up to the number 16 in base 2 (e.g. 0000 - 0, 0001 - 1, 0010 - 2 , etc ). Where it begins to get interesting is when all of our symbols don't occur with equal probability. To get a sense of this situation, I'll show 5 example outputs:

'000001000100000000010000010000'

'000000000010000000000001000000'

'010100000000000000000000111000'

'010100000000000000000000111000'

'000000000100000000110000000010'

looking at these examples, it begins to become clear that since we have a lot more zeros than ones, each of these messages contain less information than the case when 0 and 1 occur with equal probability. In fact, in this case, if 0 occurs 90% of the time, and 1 occurs 10% of the time, the shannon entropy comes out to be 0.47. Meaning each symbol is worth just less than half a bit. We should expect our messages in this case to have to be about twice as long to encode the same amount of information. In an extreme example, imagine you were trying to transmit a message to someone in binary, but for some reason, your device had a sticky 0 key so that every time you pushed 0, it transmitted 0 10 times in a row. It should be clear in this case that as far as the receiver is concerned, this is not a very efficient transmission scheme.

English

What does this have to do with anything? Well, all of that and I really only wanted to build up a fact you already know. The fact is, the English language is not very efficient on a per symbol basis. For example, I'm sure everyone knows exactly what word will come at the end of this _. There you go, I was able to express exactly the same thought with at least 8 fewer characters. n fct, w cn d _ lt bttr [in fact, we can do a lot better], using 22 characters to express a thought that normally takes 31 characters. In fact, Shannon has a nice paper where he attempted to measure the entropy of the english language itself. Using more sophisticated methods, he concludes that english has an information entropy of between 0.6 and 1.3 bits per character, let's call it 1 bit per character. Whereas, if each of the 27 symbols (26 letters + space) we commonly use each showed up equally frequently, we would have 4.75 bits per character possible. Of course, from a practical communication standpoint, having redundancies in human language can be a useful thing, as it allows us to still understand one another even over noisy phone lines and with very bad handwriting. But, with modern computers and faithful transmission of information, we really ought to be able to do better.

Twitter

This brings me back to twitter. If you are unaware, twitter allows users to post short, 140 character messages for the rest of the world to enjoy. 140 characters is not a lot to go on. Assuming 4.5 characters per word, this means that in traditionally written english you're lucky to fit 25 words in a standard tweet. But, we know now that we can do better. In fact, if we could come up with some kind of crazy scheme to compress english in such a way as to use each of the 27 usual characters so that each of those characters appeared with roughly equal probability, we've seen that we could get 4.75 bits per character, with 140 characters and 5.5 symbols per word, this would allow us to fit not 25 words in a tweet but 120 words. A factor of 4.8 improvement. Of course we would have to discover this miraculous encryption transformation. Which to my knowledge remains undiscovered. But, we can do better. It turns out that twitter allows you to use Unicode characters in your tweets. Beyond enabling you to talk about Lagrangians (ℒ) and play cards (♣), it enables international communication, by including foreign alphabets. So, in fact we don't need to limit ourselves to the 27 commonly used English symbols. We could use a much larger alphabet, Chinese say. I choose Chinese because there are over 20,900 Chinese alphabet symbols in Unicode. Using all of these characters, we could theoretically encode 14.3 bits of information per character, with 140 characters, and 1 bit per English character, and 5.5 symbols per English word, we could theoretically fit over 365 English words in a single tweet. But alas, we would have to discover some magical encoding algorithm that could map typed English to the Chinese alphabet such that each of the Chinese symbols occurred with equal probability. I wasn't able to do that well, but I did make an attempt.

My Attempt

So, I tried to compress the English language, an design an effective mapping from written English to the Chinese character set of Unicode. We know that we aim to have each of these Chinese characters occur with equal probability, so my algorithm was quite simple. Let's just look at a bunch of English and see which pair of characters occur with the highest probability, and map these to the first Chinese character in the Unicode set. Replace their occurring in the text, rinse, and repeat. This technique is guaranteed to reduce the probability at which the most common character occurs at every step, by taking some if its occurrences and replacing them, so it at least aims to achieve our ultimate goal. That's it. Of course, I tried to bootstrap the algorithm a little bit by first mapping the most common 1500 words to their own symbols. For example, consider the first stanza of the Raven by Edger Allen Poe

Once upon a midnight dreary, while I pondered, weak and weary,

Over many a quaint and curious volume of forgotten lore--

While I nodded, nearly napping, suddenly there came a tapping,

As of some one gently rapping, rapping at my chamber door.

"'Tis some visiter," I muttered, "tapping at my chamber door--

                     Only this and nothing more."

The most common character is ' ' (the space). The most common pair is 'e ' (e followed by space), so let's replace 'e ' with the first Chinese Unicode character '一' we obtain:

Onc一upon a midnight dreary, whil一I pondered, weak and weary,

Over many a quaint and curious volum一of forgotten lore--

Whil一I nodded, nearly napping, suddenly ther一cam一a tapping,

As of som一on一gently rapping, rapping at my chamber door.

"'Tis som一visiter," I muttered, "tapping at my chamber door--

                     Only this and nothing more.'

So we've reduced the number of spaces a bit. Doing one more step, now the most common pair of characters is 'in', which we replace by '丁' obtaining:

Onc一upon a midnight dreary, whil一I pondered, weak and weary,

Over many a qua丁t and curious volum一of forgotten lore--

Whil一I nodded, nearly napp丁g, suddenly ther一cam一a tapp丁g,

As of som一on一gently rapp丁g, rapp丁g at my chamber door.

"'Tis som一visiter," I muttered, "tapp丁g at my chamber door--

                     Only this and noth丁g more.'

etc. The end results of the effort are demo-ed here. Feel free to play around with it. For the most part, typing some standard English, I seem to be able to get compression ratios around 5 or so. Let me know how it does for you. I'll leave you with this final message:

儌咹乺悃巄格丌凣亥乄叜

Python code that I used to do the heavy lifting is available as a gist.

The rotting corpses of sunbeams cause global warming.

Good news, everyone! While rummaging through all my old stuff at home, I found my long-lost copy of Toto IV. Huzzah for me! This is entirely unrelated to what I wanted to talk about, but I have it on good authority that Toto's Africa syncs up really well with this post [1]. I'll tell you when to press play. Anyway, what I really wanted to talk about was a fairly well-posed problem in Futurama. In the episode "Crimes of the Hot," all of the Earth's robots vent their various "exhausts" into the sky at the same time, using the thrust to push the Earth into an orbit slightly further away from the sun. As a result of this new orbit, the year is made longer by "exactly one week." Anything that quantitative is pretty much asking to be analyzed. Let's explore this problem a bit more then, why not? [ Those wishing to get the full aural experience of this post should pressplay on their cassette players ... now ] First, a little background. In this episode, it is learned that all the robots (especially Hedonism Bot) emit the greenhouse gases responsible for Global Warming. The previous solution (detailed here) is no longer viable, so it is decided that all robots must be destroyed (especially Hedonism Bot). The disembodied head of Richard Nixon rounds up all the world's robots on the Galapagos [2] to have a "party" so that they may be destroyed by a giant space-based electromagnetic pulse cannon. In a last-ditch effort to save the robots, Professor Farnsworth has all the robots blast their exhausts into the sky, using the thrust to push the Earth into an orbit further away from the sun, thus solving the problem of global warming once and for all. As a result of changing the Earth's orbit, the year is "exactly one week longer." First Pass Through Ok, so what can we say about the new orbit if all we know is that its orbital period is exactly one week longer? Well, we know from our good buddy Kepler that the square of the period of a bound orbit is proportional to the cube of its semi-major axis [3], so $$\tau^2 \propto a^3.$$ We already know the Earth's period (1 year) and semi-major axis (1 AU) before the robo-boost, so we can get rid of the proportionality by writing things in terms of the initial values. In other words, $$ \left(\frac{\tau}{1\~\mbox{yr}}\right)^2=\left(\frac{a}{1\~\mbox{AU}}\right)^3.$$ Alright, so we know that our new orbital period is 1 year + 1 week, or since there are 52 weeks in a year, 53/52 years. So our new semi-major axis is $$ a = \left(\frac{1 + 1/52\~\mbox{yr}}{1\~\mbox{yr}}\right)^{2/3}\mbox{AU}\approx1.013\~\mbox{AU},$$ or a little over 1% larger than it is currently. Fair enough. So would this fix Global Warming for ever and ever? Let's see. The solar flux at some distance d is given by $$ S = \frac{L_{\odot}}{4\pi d^2}, $$ where L is the luminosity of the sun. So the ratio of the flux at the new semi-major axis [4] to that before the orbit was changed is $$ \frac{S}{S_0}=\left(\frac{a_0}{a}\right)^2=\left(\frac{a}{1\~\mbox{yr}}\right)^{-2}.$$ OK, so we have the flux, but how do we relate this to temperature? Well, we know that the power radiated by a blackbody of temperature T is given by $$ P = \sigma A T^4, $$ where sigma is the Stefan-Boltzmann constant, A is the area of the emitting region and T is the temperature. For a blackbody in equilibrium, the power coming in is going to be equal to the power going out. The power coming in is just the solar flux times the cross-section area of Earth, given by $$ P_{in} = S\times\pi R^2_{\oplus} $$ and the power going out is just that radiated by the Earth as a blackbody $$ P_{out} =\sigma \times 4\pi R^2_{\oplus}\times T^4. $$ Equating the power in to the power out gives $$ T = \left( \frac{S}{4\sigma}\right)^{1/4}. $$ Now we can find the ratio of the new average Earth temperature to the temperature before the orbital move. We have $$ \frac{T}{T_0} =\left( \frac{S}{S_0}\right)^{1/4}=\left( \frac{a_0}{a}\right)^{1/2}\approx0.994$$ If we take the initial average Earth temperature to be something like T = 300 K, then we find a new temperature of T = 298 K. Huzzah, a whole 2 degrees cooler! That may not sound like a lot, but remember, that's the mean global temperature. Apparently, it only takes a few degrees increase in global average temperatures to make things a bit uncomfortable for people. The IPCC indicates that the average global surface temperature on Earth in the next century is likely to rise by about 1 to 2 degrees under optimistic scenarios or about 3 to 6 degrees under pessimistic scenarios. So the robo-boost option is at least in the right ballpark here. Neat! How Big Is The Push? So how big of a push did the robots need to give the Earth to boost it out to this new orbit? Is this possible? Let's find out! First we need to find out how the Earth's velocity has changed. We can do this by finding the change in energy. The total energy of a bound orbit is given by $$ E = -\frac{k}{2a}$$ where a is the semi-major axis of the orbit and k= GMm. So the difference in Earth's energy before and after the robo-boost is $$ E_f - E_0 =-\frac{k}{2a_f}-\left(-\frac{k}{2a_0}\right)=\frac{k}{2a_0}\left(1-\frac{a_0}{a_f}\right).$$ But we also know that Earth's energy in the orbit is given by $$ E = -\frac{k}{r} + \frac{1}{2}mv^2, $$ so the difference in energy before and after is $$ E_f - E_0 =\frac{1}{2}m\left(v^2_f-v^2_0\right), $$ where we have found the energies immediately before and immediately after the boost so Earth is pretty much at the same distance from the sun, so the potential energy terms cancel. Combining our expressions for the change in energy and solving for the final velocity, we find $$ v_f = \left[\frac{GM_{\odot}}{a_0}\left(1-\frac{a_0}{a_f}\right)+v^2_0\right]^{1/2}.$$ Taking the initial orbital velocity of the Earth to be 30 km/s, we find that the final velocity of the Earth immediately after the robo-boost is $$ v_f = 30.2\~\mbox{km/s}$$ So the robots just need to give a "little" 200 m/s boost to the Earth, right? Well, we are adding velocity vectors here, so it depends on which direction the robots are pushing. The magnitude of the final velocity is given by $$v_f = \sqrt{\left({\bf v_0}+{\bf \Delta v} \right)^2}=\sqrt{v^2_0+\Delta v^2-2v_0\Delta v \cos{\beta}},$$ where delta v is the boost in velocity caused by the robots and beta is the angle between the initial orbital motion of the Earth and the velocity boost from the robots. If they wanted to make it slightly easier on themselves, the robots would have boosted the Earth in the direction it was already moving. That would make the cosine beta term equal to one and thus minimize the necessary boost. However, in the show the robots appear to point their exhaust right at the sun (see figure below). This is essentially at a 90 degree angle to the Earth's orbital motion, so the cosine beta term goes to zero in our expression above. Plugging it all in we find that the magnitude of the robo-boost is $$\Delta v \approx 3.5\~\mbox{km/s}.$$ We see that this is a fair bit larger than the 0.2 km/s needed for a boost parallel to Earth's initial velocity.

Robots blasting from the Galapagos (which now appear to be in China...)

Alright, so how much effort would it take to give that kind of boost to the Earth? We can quantify this effort in terms of a force or in terms of the energy difference. Let's do both. For the force, we have $$ F = \frac{\Delta p}{\Delta t}=\frac{M_{\oplus}\Delta v}{\Delta t}.$$ Here we are a little stuck unless we can figure out the duration of the robo-boost. Watching the episode again, the robots are blasting up exhaust for about a minute but then the show cuts to commercial. So we don't really know how long they were pushing. Let's just say an hour, but we'll leave the time in if we want to fiddle with that. Plugging in numbers, the total force is $$ F = 6\times10^{24}\~\mbox{N}\left(\frac{\Delta t}{1\~\mbox{hr}}\right)^{-1}.$$ If this force is spread evenly over the billion robots present [5], then each robot would be applying a force of $$ F = 6\times10^{15}\~\mbox{N},$$ which is roughly equivalent to the force it would take to lift up Mount Everest [6]. That wasn't terribly helpful. Let's look at the work then instead. The total work done by the robots to move the Earth is $$ W = \frac{1}{2}M_{\oplus}\left(v^2_f - v^2_0\right) \approx 4\times10^{31}\~\mbox{J}.$$ Well, that's a large number. Could a billion robots feasibly do that much work? If the robots are each 100 kg, then if the mass of all billion robots were directly converted to energy, we would get $$ E = mc^2 = 10^9\times10^2\~\mbox{kg}\times\left(3\times10^8\~\mbox{m/s}\right)^2 \approx 10^{28}\~\mbox{J},$$ or less than a thousandth the total energy needed. So it looks unlikely that the robots would be able to push the Earth, but that was to be expected. Changes to The Orbit Let's take a look at how the robo-boost affects the entirety of the Earth's new orbit. In our first pass through the problem, we ignored the fact that the shape of the orbit changed and only focused on the new semi-major axis. To see why we must also consider the changes to the "shape" of the orbit, take a look at the figure below. In the figure, the initial orbit is plotted (black dashed line) as well as two new orbits that each have the appropriate semi-major axis so that the period of revolution is one year and one week. The difference between the two final orbits comes from the robots pushing in different directions. In the blue orbit, the boost was made in a direction radially outward from the Sun (that is, perpendicular to the orbital velocity of the Earth). This is the case shown in the Futuramaepisode. In the red orbit, the boost was made parallel to the orbital velocity of the Earth. In each case, the boost was applied at the point labeled with an "X." One thing that jumps out from this figure is that the Earth is always further away from the sun on the red orbit than it was on the initial (dashed black) orbit. But on the blue orbit, the Earth is further away from the Sun than it was initially for only half the orbit. On the other half, the blue orbit would actually make the Earth's temperature higher than it was on the old orbit! The temperature calculation we made earlier should hold pretty well for the red orbit, since it is essentially a circle. It would be a little more tricky for the blue orbit, as one would need to get a time-averaged value of the flux over the course of the whole orbit. A hundred Quatloos to anyone that does the calculation. Wrap-Up So what have we found out here? Well, it seems that there are certain scenarios in which boosting the Earth out to a new orbit with period of 1 year + 1 week could cool the Earth by a few degrees. Granted, we have made some simplifications (the Earth is not a blackbody), but the general idea of the thing should still hold. I had some fun playing around with this problem and I thought it was neat that there was a good deal of information to get started with from the episode. The Futurama people gave an exact period and at least a visual representation of the direction the robots apply their push. So 600 Quatloos for the writers! Not Quite As Useless as Usual Footnotes [1] At least I think it says so if you play this song backwards. [2] According to the Wikipedia page for the episode, the location of the Galapagos for the party was chosen because the writers felt that it would be most convenient to push the Earth near the equator. [3] The semi-major axis of an ellipse is half of the longest line cutting through the center of the ellipse. Likewise, the semi-minor axis is half of the shortest line drawn through the center of the ellipse. Check this out for some more fun stuff on ellipses. [4] This is technically incorrect, since the semi-major axis is measured from the center of the ellipse, but the sun is located on one of the foci. However, this requires information on the eccentricity of the orbit, which we are currently glossing over right now. Our method is then approximate, but becomes exact in the case where both orbits are circles. The effect, however, is minor. At worst, it is semi-minor. Zing! [5] My source for this billion robots number comes from Professor Farnsworth himself. When it looks like the robots will all be destroyed the Professor says "A billion robot lives are about to be extinguished. Oh, the Jedis are going to feel this one!" [6] Well, sort of. The height of Everest is \~10^4 m, so this gives a volume of \~10^12 m^3. The density of most metals is around \~10 g/cm^3, which is \~10^4 kg/m^3. This gives a mass of \~10^16 kg. The weight is then \~10^17 N. Each robot exerts a force of \~10^16 N. So not quite, but hey it was the first thing I thought of and it almost worked out so I'm sticking with it!

Have you ever sat on a beach and wondered how many grains of sand there were? I have, but I may be a special case. Today we're going to take that a step further, and figure out how many grains of sand there are on the entire earth. (Caveat: I'm only going to consider sand above the water level, since I don't have any idea what the composition of the ocean floor is). I'm going to start by figuring out how much beach there is in the world. If you look at a map of the world, there are four main coasts that run, essentially, a half circumference of the world. We'll say the total length of coast the world has is roughly two circumferences. As an order of magnitude, I would say that the average beach width is 100 m, and the average depth is 10 m. This gives a total beach volume of $$ (100 m)(10 m)(4 \pi (6500 km) )= 82 km^3$$ That's not a whole lot of volume. Let's think about deserts. The Sahara desert is by far the largest sandy desert in the world. Just as a guess, we'll assume that the rest of the sandy deserts amount to 20% (arbitrary number picked staring at a map) as much area as the Sahara. According to wikipedia the area of the Sahara is 9.4 million km^2. We'll take, to an order of magnitude, that the sand is 100 m deep. 10 m seems to little, and 1 km too much. That amounts to \~1 million km^3 of sand. We're going to assume that a grain of sand is about 1 mm in radius The volume occupied by a grain of sand is then 1 mm^3. Putting that together with our previous number for the occupied volume gives $$ \frac{1\cdot 10^6 km^3}{1 mm^3}=\frac{1 \cdot 10^{15}}{1\cdot 10^{-9}}=1\cdot 10^{24}$$ That's a lot of grains of sand. Addendum: Carl Sagan is quoted as saying

"The total number of stars in the Universe is larger than all the grains of sand on all the beaches of the planet Earth"

If we just use our beach volume, that gives a total number of grains of sand as \~1*10^20, which is large, but not as large as what we found above. Is that less than the number of stars in in the universe? Well, that's a question for another day (or google), but the answer is, to our best estimate/count, yes.

Citizen's Bank Park

I like baseball. Well, technically, I like laying[3] lying on the couch for three hours half-awake eating potato chips and mumbling obscenities at the television. But let's not split hairs here. Anyway, out of curiosity and in partial atonement for the sins of my past [1] I would now like to do a quick calculation to see how much effect the Coriolis force has on a home-run ball. The Coriolis force is one of the artificial forces we have to put in if we are going to pretend the Earth is not rotating. For a nice intuitive explanation of the Coriolis force see this post over at Dot Physics. Let's now consider the following problem. Citizen's Bank Park (home to the Philadelphia Phillies) is oriented such that the line from home plate to the foul pole in left field runs essentially South-North. Imagine now that Ryan Howard hits a hard shot down the third base line (that is, he hits the ball due North). Assuming it is long enough to be a home run, how with the Coriolis force effect the ball's trajectory? This is a well-posed problem and we could solve it as exactly as we wanted. But please don't make me. It's icky and messy and I don't feel like it. So let's do some dimensional analysis! Hooray for that! So what are the relevant physical quantities in this problem? Well, we'll certainly need the angular velocity of the Earth and the speed of the baseball. We'll also need the acceleration due to gravity. Alright, so what do we want to get out of this? Well, ideally we'd like to find the distance the ball is displaced from its current trajectory. So is there any way we can combine an angular velocity, linear velocity and acceleration to get a displacement? Let's see. We can write out the dimensions of each in terms of some length, L, and some time, T. So: $$ \left[ \Omega \right] = \frac{1}{T} $$ $$ \left[ v \right] = \frac{L}{T} $$ $$ \left[ g \right] = \frac{L}{T^2} $$ where we have used the notation that [some quantity] = units of that quantity. Combining these in a general way gives: $$ L = \left[ v^{\alpha} \Omega^{\beta} g^{\gamma} \right] = \left( \frac{L}{T}\right)^{\alpha}\left( \frac{1}{T}\right)^{\beta}\left( \frac{L}{T^2}\right)^{\gamma} = L^{\alpha+\gamma} T^{-(\alpha+\beta+2\gamma)}$$ Since we want just want a length scale here, we need: $$\alpha+\gamma = 1\~\~\~\mbox{and}\~\~\~\alpha+\beta+2\gamma = 0. $$ We can fiddle around with the above two equations to get two new equations that are both functions of alpha. This gives: $$\beta = \alpha - 2\~\~\~\mbox{and}\~\~\~\gamma = 1 - \alpha. $$ Unfortunately, we have two equations and three unknowns, so we have an infinite number of solutions. I've listed a few of these in the Table below.

Ways of getting a length

At this point, we have taken Math as far as we can. We'll now have to use some physical intuition to narrow down our infinite number of solutions to one. Hot dog! One way we can choose from these expressions is to see which ones have the correct dependencies on each variable. So let's consider what we would expect to happen to the deflection of our baseball by the Coriolis force if we changed each variable. What happens if we were to "turn up" the gravity and make g larger? If we make g much larger, then a baseball hit at a given velocity will not be in the air as long. If the ball isn't in the air as long, then it won't have as much time to be deflected. So we would expect the deflection to decrease if we were to increase g. This suggests that g should be in the denominator of our final expression. What happens if we turn up the velocity of the baseball? If we hit the ball harder, then it will be in the air longer and thus we would expect it to have more time to be deflected. Since increasing the velocity would increase the deflection, we would expect v to be in the numerator. What happens if we turn up the rotation of the Earth? Well, if the Earth is spinning faster, it's able to rotate more while the ball is in the air. This would result in a greater deflection in the baseball's path. Thus, we would expect this term to be in the numerator. So, using the above criteria, we have eliminated everything on that table with alpha less than 3 based on physical intuition. Unfortunately, we still have an infinite number of solutions to choose from (i.e. all those with alpha greater than or equal to 3). But, we DO have a candidate for the "simplest" solution available, namely the case where alpha = 3. Since we have exhausted are means of winnowing down our solutions, let's just go with the alpha = 3 case. Our dimensional analysis expression for the deflection of a baseball is then $$ \Delta x \sim \frac{v^3 \Omega}{g^2} $$ Plugging in typical values of $$ v = 50\~\mbox{m/s}\~\~\~(110\~\mbox{mi/hr}) $$ $$ \Omega = 7 \times 10^{-5}\~\mbox{rad/s} $$ $$ g = 9.8\~\mbox{m/s}^2 $$ we get $$ \Delta x \approx 0.1\~\mbox{m} = 10\~\mbox{cm}. $$ That's all fine and good, but which way does the ball get deflected? Is it fair or foul? Well, remembering that the Coriolis force is given by: $$ {\bf F} = -2m{\bf \Omega} \times {\bf v} $$ and utilizing Ye Olde Right Hand Rule, we see that a ball hit due north will be deflected to the East. In the case of Citizen's Bank Park, that is fair territory. But how good is our estimate? Well, I did the full calculation (which you can find here) and found that the deflection due to the Coriolis force is given by $$ \Delta x =-\frac{4}{3}\frac{\Omega v^3_0}{g^2} \cos \phi \sin^3 \alpha \left[1 -3 \tan \phi \cot \alpha \right] $$ where phi is the latitude and alpha is the launch angle of the ball. We see that this is essentially what we found by dimensional analysis up to that factor of 4/3 and some geometrical terms. Not bad! Plugging in the same numbers we used before, along with the appropriate latitude and a 45 degree launch angle we find that the ball is deflected by: $$ \Delta x = 5\~\mbox{cm}. $$ For comparison, we note that the diameter of a baseball is 7.5 cm. So in the grand scheme of things, this effect is essentially negligible. [2] That wraps up the calculation, but I'm certain that many of you are still a little wary of this voodoo calculating style. And you should be! Although dimensional analysis will give you a result with the proper units and will often give you approximately the right scale, it is not perfect. But, it can be formalized and made rigorous. The rigorous demonstration for dimensional analysis is due to Buckingham and his famous pi-theorem. The original paper can be found behind a pay-wall here and a really nice set of notes can be found here. It's a pretty neat idea and I highly recommend you check it out! Unnecessary Footnotes: [1] Once in college I argued with a meteorologist named Dr. Thunder over the direction of the Coriolis force on a golf ball for the better half of the front nine at Penn State's golf course. I was wrong. Moral of the story: don't play golf with meteorologists. [2] For a counterargument, see Fisk et al. (1975) [3] Text has been corrected to illustrate our enlightenment by a former English major as to the difference between 'lay' and 'lie' through the following story: 'Once in a college psych class, a young student said "It's too hot. Let's lay down." A mature student, a journalist, asked, "Who's Down?" '