Physics has greatly influenced the progress of most sports. There have been continual improvements in equipment for safety or performance as well as improvements in technique. I'd like to talk about some physics in sports over a series of posts. Here I'll talk about a technique improvement in High Jumping, the Fosbury Flop. The Fosbury Flop came into the High Jumping scene in the 1968 Olympics, where Dick Fosbury used the technique to win the gold medal. The biggest difference between the Flop and previous methods is that the jumper goes over the bar upside down (facing the sky). This allows the jumper to bend their back so that their arms and legs drape below the bar which lowers the center of mass (See the picture above). Here is a video of the Fosbury Flop executed very well. 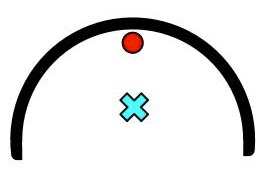Let’s assume Dick Fosbury is shaped like a semi-circle as he moves over the bar. The bar is indicated as a red circle, as this is a side view. From this diagram, we can guess his center of mass is probably near the marked 'x', since most of his mass is below the bar. It is important to recall the definition of center of mass, which is the average location of all of the mass in an object. $$ \vec{R} = \frac{1}{M} \int \vec{r} dm $$ Note that this is a vector equation, and the integral should be over all of the mass elements. This integral gets easier because I'm going to assume that Dick Fosbury is a constant density semi-circle. This means that $$ M = Ch $$ where C is a constant equal to the ratio of the mass to the height, and $$dm = C * dh $$. This is a vector equation, so in principle we need to solve the x integral and the y integral; however, due to the symmetry about the y-axis, the x integral is zero. Finally we'll convert to polar coordinates, leaving us with: $$ y = \frac{1}{C \pi R} \int_0^\pi R\sin{\theta} C R d\theta = \frac{1}{C \pi R} R (-\cos{\theta}) C R \bigg|_0^\pi = \frac{2R}{\pi} $$ Ok, so this is the y-coordinate of the center of mass of our jumper relative to the bottom of the semi-circle. Now we need to calculate relative to the top of the bar, which is roughly the location of the top of the circle. We just need to subtract from R: $$ R - \frac{2}{\pi} R = R * (1 - \frac{2}{\pi}) = \frac{h}{\pi} * (1 - \frac{2}{\pi}) $$ Now Dick Fosbury was 1.95m tall, which gives us a distance of 22.6 cm BELOW the bar! Of course he's not a semi-circle, but this isn't a terrible approximation, as you can see from the video linked above. Further, wikipedia mentions that some proficient jumpers can get their center of mass 20 cm below the bar, which matches pretty well with our guess. A nifty technique in physics is looking at the point-particle system, which allows us to see the underlying motion of a system. If you’re not familiar with this method, you collect any given number of objects and replace them with a single point at the center of mass of the object. We can use energy conservation now for our point-mass instead of the entire body of the jumper.^note^ In this case, we can simply deal with the center of mass motion of the jumper. All of my kinetic energy will be converted to gravitational potential energy. Again this is an approximation because some energy is spent on forward motion, as well as the slight twisting motion which I'll ignore. $$E = \frac{1}{2} mv^2 = mgh$$ Now let’s look at some data. Here is a plot of each world record in the high jump. 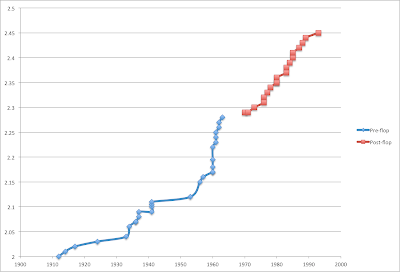The blue data show jumps before the Flop, and the red data show records after the Flop. Note: In 1978, the straddle technique broke the world record, being the only non-flop technique to do so since 1968. Thanks Janne! The Flop was revealed in 1968, so I’ll assume that all jumps before this year used a method where the center of mass of the jumper was roughly even with the bar, while all jumps after this year used the flop (see the previous note). Clearly something happened just before the Flop came out, and this is something called the Straddle technique. I want to know the percent difference in the initial energies required, so I will calculate $$ 100\% * \frac{E_0-E_f}{E_0} = 100\% \frac{mgh_0-mgh_f}{mgh_0} = 100\% * \frac{h_0-h_f}{h_0} $$ where $$E_0$$ is the initial energy without the force, err the flop, and $$ E_f $$ is the initial energy using the flop. Since we are using the point-particle system, the gravitational potential energy only cares about the center of mass of the flopper, and we need to know the height of the center of mass for a 2.45m flop, which is the current world record. This corresponds to a flop center of mass height of 2.25m, which gives us an 8.2% decrease in energy using the flop (versus a method where the center of mass is even with the bar)! The current world record is roughly 20 cm higher than it was when the flop came out. This could be due to athletes getting stronger, but this physics tells us that some of the height increase could have been from the technique change. To sum up, the high jump competition, along with many other sports, is being exploited by physics! [note] Here we're relying on the center of mass being equal to something called the center of gravity of the jumper. The center of mass is as defined above. The center of gravity is the average location of the gravitational force on the body. This happens to be the same as the center of mass if you assume we are in a uniform gravitational field, which is essentially true on the surface of the Earth.

Comments