Futurama Physics

The rotting corpses of sunbeams cause global warming.

Good news, everyone! While rummaging through all my old stuff at home, I found my long-lost copy of Toto IV. Huzzah for me! This is entirely unrelated to what I wanted to talk about, but I have it on good authority that Toto's Africa syncs up really well with this post [1]. I'll tell you when to press play. Anyway, what I really wanted to talk about was a fairly well-posed problem in Futurama. In the episode "Crimes of the Hot," all of the Earth's robots vent their various "exhausts" into the sky at the same time, using the thrust to push the Earth into an orbit slightly further away from the sun. As a result of this new orbit, the year is made longer by "exactly one week." Anything that quantitative is pretty much asking to be analyzed. Let's explore this problem a bit more then, why not? [ Those wishing to get the full aural experience of this post should pressplay on their cassette players ... now ] First, a little background. In this episode, it is learned that all the robots (especially Hedonism Bot) emit the greenhouse gases responsible for Global Warming. The previous solution (detailed here) is no longer viable, so it is decided that all robots must be destroyed (especially Hedonism Bot). The disembodied head of Richard Nixon rounds up all the world's robots on the Galapagos [2] to have a "party" so that they may be destroyed by a giant space-based electromagnetic pulse cannon. In a last-ditch effort to save the robots, Professor Farnsworth has all the robots blast their exhausts into the sky, using the thrust to push the Earth into an orbit further away from the sun, thus solving the problem of global warming once and for all. As a result of changing the Earth's orbit, the year is "exactly one week longer." First Pass Through Ok, so what can we say about the new orbit if all we know is that its orbital period is exactly one week longer? Well, we know from our good buddy Kepler that the square of the period of a bound orbit is proportional to the cube of its semi-major axis [3], so $$\tau^2 \propto a^3.$$ We already know the Earth's period (1 year) and semi-major axis (1 AU) before the robo-boost, so we can get rid of the proportionality by writing things in terms of the initial values. In other words, $$ \left(\frac{\tau}{1\~\mbox{yr}}\right)^2=\left(\frac{a}{1\~\mbox{AU}}\right)^3.$$ Alright, so we know that our new orbital period is 1 year + 1 week, or since there are 52 weeks in a year, 53/52 years. So our new semi-major axis is $$ a = \left(\frac{1 + 1/52\~\mbox{yr}}{1\~\mbox{yr}}\right)^{2/3}\mbox{AU}\approx1.013\~\mbox{AU},$$ or a little over 1% larger than it is currently. Fair enough. So would this fix Global Warming for ever and ever? Let's see. The solar flux at some distance d is given by $$ S = \frac{L_{\odot}}{4\pi d^2}, $$ where L is the luminosity of the sun. So the ratio of the flux at the new semi-major axis [4] to that before the orbit was changed is $$ \frac{S}{S_0}=\left(\frac{a_0}{a}\right)^2=\left(\frac{a}{1\~\mbox{yr}}\right)^{-2}.$$ OK, so we have the flux, but how do we relate this to temperature? Well, we know that the power radiated by a blackbody of temperature T is given by $$ P = \sigma A T^4, $$ where sigma is the Stefan-Boltzmann constant, A is the area of the emitting region and T is the temperature. For a blackbody in equilibrium, the power coming in is going to be equal to the power going out. The power coming in is just the solar flux times the cross-section area of Earth, given by $$ P_{in} = S\times\pi R^2_{\oplus} $$ and the power going out is just that radiated by the Earth as a blackbody $$ P_{out} =\sigma \times 4\pi R^2_{\oplus}\times T^4. $$ Equating the power in to the power out gives $$ T = \left( \frac{S}{4\sigma}\right)^{1/4}. $$ Now we can find the ratio of the new average Earth temperature to the temperature before the orbital move. We have $$ \frac{T}{T_0} =\left( \frac{S}{S_0}\right)^{1/4}=\left( \frac{a_0}{a}\right)^{1/2}\approx0.994$$ If we take the initial average Earth temperature to be something like T = 300 K, then we find a new temperature of T = 298 K. Huzzah, a whole 2 degrees cooler! That may not sound like a lot, but remember, that's the mean global temperature. Apparently, it only takes a few degrees increase in global average temperatures to make things a bit uncomfortable for people. The IPCC indicates that the average global surface temperature on Earth in the next century is likely to rise by about 1 to 2 degrees under optimistic scenarios or about 3 to 6 degrees under pessimistic scenarios. So the robo-boost option is at least in the right ballpark here. Neat! How Big Is The Push? So how big of a push did the robots need to give the Earth to boost it out to this new orbit? Is this possible? Let's find out! First we need to find out how the Earth's velocity has changed. We can do this by finding the change in energy. The total energy of a bound orbit is given by $$ E = -\frac{k}{2a}$$ where a is the semi-major axis of the orbit and k= GMm. So the difference in Earth's energy before and after the robo-boost is $$ E_f - E_0 =-\frac{k}{2a_f}-\left(-\frac{k}{2a_0}\right)=\frac{k}{2a_0}\left(1-\frac{a_0}{a_f}\right).$$ But we also know that Earth's energy in the orbit is given by $$ E = -\frac{k}{r} + \frac{1}{2}mv^2, $$ so the difference in energy before and after is $$ E_f - E_0 =\frac{1}{2}m\left(v^2_f-v^2_0\right), $$ where we have found the energies immediately before and immediately after the boost so Earth is pretty much at the same distance from the sun, so the potential energy terms cancel. Combining our expressions for the change in energy and solving for the final velocity, we find $$ v_f = \left[\frac{GM_{\odot}}{a_0}\left(1-\frac{a_0}{a_f}\right)+v^2_0\right]^{1/2}.$$ Taking the initial orbital velocity of the Earth to be 30 km/s, we find that the final velocity of the Earth immediately after the robo-boost is $$ v_f = 30.2\~\mbox{km/s}$$ So the robots just need to give a "little" 200 m/s boost to the Earth, right? Well, we are adding velocity vectors here, so it depends on which direction the robots are pushing. The magnitude of the final velocity is given by $$v_f = \sqrt{\left({\bf v_0}+{\bf \Delta v} \right)^2}=\sqrt{v^2_0+\Delta v^2-2v_0\Delta v \cos{\beta}},$$ where delta v is the boost in velocity caused by the robots and beta is the angle between the initial orbital motion of the Earth and the velocity boost from the robots. If they wanted to make it slightly easier on themselves, the robots would have boosted the Earth in the direction it was already moving. That would make the cosine beta term equal to one and thus minimize the necessary boost. However, in the show the robots appear to point their exhaust right at the sun (see figure below). This is essentially at a 90 degree angle to the Earth's orbital motion, so the cosine beta term goes to zero in our expression above. Plugging it all in we find that the magnitude of the robo-boost is $$\Delta v \approx 3.5\~\mbox{km/s}.$$ We see that this is a fair bit larger than the 0.2 km/s needed for a boost parallel to Earth's initial velocity.

Robots blasting from the Galapagos (which now appear to be in China...)

Alright, so how much effort would it take to give that kind of boost to the Earth? We can quantify this effort in terms of a force or in terms of the energy difference. Let's do both. For the force, we have $$ F = \frac{\Delta p}{\Delta t}=\frac{M_{\oplus}\Delta v}{\Delta t}.$$ Here we are a little stuck unless we can figure out the duration of the robo-boost. Watching the episode again, the robots are blasting up exhaust for about a minute but then the show cuts to commercial. So we don't really know how long they were pushing. Let's just say an hour, but we'll leave the time in if we want to fiddle with that. Plugging in numbers, the total force is $$ F = 6\times10^{24}\~\mbox{N}\left(\frac{\Delta t}{1\~\mbox{hr}}\right)^{-1}.$$ If this force is spread evenly over the billion robots present [5], then each robot would be applying a force of $$ F = 6\times10^{15}\~\mbox{N},$$ which is roughly equivalent to the force it would take to lift up Mount Everest [6]. That wasn't terribly helpful. Let's look at the work then instead. The total work done by the robots to move the Earth is $$ W = \frac{1}{2}M_{\oplus}\left(v^2_f - v^2_0\right) \approx 4\times10^{31}\~\mbox{J}.$$ Well, that's a large number. Could a billion robots feasibly do that much work? If the robots are each 100 kg, then if the mass of all billion robots were directly converted to energy, we would get $$ E = mc^2 = 10^9\times10^2\~\mbox{kg}\times\left(3\times10^8\~\mbox{m/s}\right)^2 \approx 10^{28}\~\mbox{J},$$ or less than a thousandth the total energy needed. So it looks unlikely that the robots would be able to push the Earth, but that was to be expected. Changes to The Orbit Let's take a look at how the robo-boost affects the entirety of the Earth's new orbit. In our first pass through the problem, we ignored the fact that the shape of the orbit changed and only focused on the new semi-major axis. To see why we must also consider the changes to the "shape" of the orbit, take a look at the figure below. 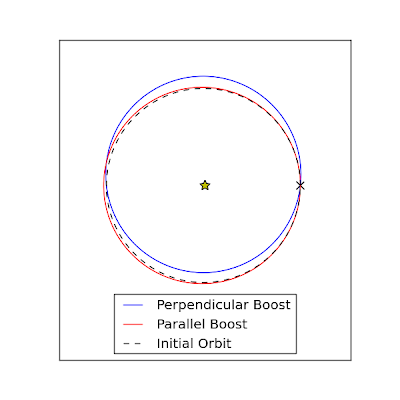In the figure, the initial orbit is plotted (black dashed line) as well as two new orbits that each have the appropriate semi-major axis so that the period of revolution is one year and one week. The difference between the two final orbits comes from the robots pushing in different directions. In the blue orbit, the boost was made in a direction radially outward from the Sun (that is, perpendicular to the orbital velocity of the Earth). This is the case shown in the Futuramaepisode. In the red orbit, the boost was made parallel to the orbital velocity of the Earth. In each case, the boost was applied at the point labeled with an "X." One thing that jumps out from this figure is that the Earth is always further away from the sun on the red orbit than it was on the initial (dashed black) orbit. But on the blue orbit, the Earth is further away from the Sun than it was initially for only half the orbit. On the other half, the blue orbit would actually make the Earth's temperature higher than it was on the old orbit! The temperature calculation we made earlier should hold pretty well for the red orbit, since it is essentially a circle. It would be a little more tricky for the blue orbit, as one would need to get a time-averaged value of the flux over the course of the whole orbit. A hundred Quatloos to anyone that does the calculation. Wrap-Up So what have we found out here? Well, it seems that there are certain scenarios in which boosting the Earth out to a new orbit with period of 1 year + 1 week could cool the Earth by a few degrees. Granted, we have made some simplifications (the Earth is not a blackbody), but the general idea of the thing should still hold. I had some fun playing around with this problem and I thought it was neat that there was a good deal of information to get started with from the episode. The Futurama people gave an exact period and at least a visual representation of the direction the robots apply their push. So 600 Quatloos for the writers! Not Quite As Useless as Usual Footnotes [1] At least I think it says so if you play this song backwards. [2] According to the Wikipedia page for the episode, the location of the Galapagos for the party was chosen because the writers felt that it would be most convenient to push the Earth near the equator. [3] The semi-major axis of an ellipse is half of the longest line cutting through the center of the ellipse. Likewise, the semi-minor axis is half of the shortest line drawn through the center of the ellipse. Check this out for some more fun stuff on ellipses. [4] This is technically incorrect, since the semi-major axis is measured from the center of the ellipse, but the sun is located on one of the foci. However, this requires information on the eccentricity of the orbit, which we are currently glossing over right now. Our method is then approximate, but becomes exact in the case where both orbits are circles. The effect, however, is minor. At worst, it is semi-minor. Zing! [5] My source for this billion robots number comes from Professor Farnsworth himself. When it looks like the robots will all be destroyed the Professor says "A billion robot lives are about to be extinguished. Oh, the Jedis are going to feel this one!" [6] Well, sort of. The height of Everest is \~10^4 m, so this gives a volume of \~10^12 m^3. The density of most metals is around \~10 g/cm^3, which is \~10^4 kg/m^3. This gives a mass of \~10^16 kg. The weight is then \~10^17 N. Each robot exerts a force of \~10^16 N. So not quite, but hey it was the first thing I thought of and it almost worked out so I'm sticking with it!