 A very cold person points out Betelgeuse
A very cold person points out Betelgeuse
Betelgeuse is a massive star at the very end of its life and could
explode any second now! Every time I hear that I get really really
excited. Like a kid in a candy store that's about to see a star blow up
like nobody's business. This giddiness will last for a solid minute
before I realize that "any second now" is taken on astronomical
timescales and roughly translates to "sometime in the next million years
maybe possibly." Then I feel sad. But you know what always cheers me up?
Calculating things! Hooray! So let's take a look at the ways Betelgeuse
could end its life (even if it's not going to happen tomorrow) and how
these would affect Earth. First, a little background. Betelgeuse is the
bright orangey-red star that sits at the head/armpit of Orion. It is one
of the brightest
stars in the night sky. Its distance has been measured by the
Hipparcossatellite to be
about 200 parsecs [1] from Earth (about 600 light years). Betelgeuse is
at least 10 times as massive as our Sun and has a diameter that would
easily accomodate the orbit of Mars. In fact, the star is big enough and
close enough that it can actually be spatially resolved by the Hubble
Space Telescope! Being so big and bright, Betelgeuse is destined to die
young, going out with a bang as a
core-collapse
supernova. This massive explosion ejects a good deal of "star stuff"
into interstellar space [2] and leaves behind either a neutron
star or a black
hole. Alright, now that we're
all caught up, let's turn our focus on this "massive explosion" bit.
What kind of energy scale are we talking about if Betelgeuse blows up?
Well, a pretty good upper bound would be if all of the star's mass (10
solar masses worth!) were converted directly to energy, so $$ E_{max} =
mc^2 =
10M_{\odot}\times\left(\frac{2\times10^{30}\~\mbox{kg}}{1\~M_{\odot}}\right)\times
\left(3\times10^8\~\mbox{m/s}\right)^2 $$ which is about $$
E_{max} \sim 10^{48}\~\mbox{J} $$ and that's nothing to shake a
stick at. But remember, this is if the entire star were converted
directly to energy, and that would be hard to do. Typical fusion
efficiencies are about \~1% [3], so let's say a reasonable estimate for
the total nuclear energy available is $$ E_{nuc} \sim \eta_{f}
\times E_{max} \sim 10^{-2} \times 10^{48}\~\mbox{J} \sim
10^{46}\~\mbox{J}. $$ This is the total energy released by a typical
supernova. As it turns out though, 99% of this energy is carried away in
the form of neutrinos and only about 1% is carried away in photons.
Since we are mainly concerned with how this explosion will affect Earth,
and the neutrinos will just pass on by, we will only consider the 1% of
energy released in photons that would reasonably interact with Earth.
That gives us $$ E_{ph} \sim 0.01 \times E_{nuc} \sim
10^{44}\~\mbox{J}. $$ Neato, so that's the total amount of energy
released in a supernova in the form of photons. How much of this energy
would be deposited at the Earth if Betelgeuse exploded? Well, if the
energy is deposited isotropically (that is, the same in all directions),
then the fluence (or time integrated energy flux) is given by $$ F_{ph}
= \frac{E_{ph}}{4\pi d^2}. $$ All this is saying is that the total
energy release by the supernova spreads out uniformly over a sphere of
radius d, so the fluence will give us the amount of energy deposited in
each square meter of that sphere (the units of fluence here are J/m^2).
The total energy deposited on Earth is then $$ E_{\oplus} = F_{ph}
\times \pi R^2_{\oplus}. $$ Hot dog! Let's plug in some numbers,
already. The total energy deposited on the Earth by a symmetrically
exploding Betelgeuse at a distance of d = 200 pc (where 1 pc = 3
10^16 m) is $$E_{\oplus}=\frac{E_{ph}}{4\pi d^2}\times\pi
R^2_{\oplus}\sim
10^{19}\~\mbox{J}\left(\frac{E_{ph}}{10^{44}\~\mbox{J}}\right)\left(\frac{d}{200\~\mbox{pc}}\right)^{-2}.$$
Well, 10^19 J certainly seems* like a lot of energy. In fact, it is
roughly the amount of energy contained in the entire nuclear arsenal of
the United States [4]. But it is spread over the entire atmosphere. Is
there a way to gauge how this would affect life on Earth? We could see
how much it would heat up the atmosphere using specific heats: $$ E =
m_{atm}c_{air}\Delta T $$ where c is the specific heat of air
(\~10^3 J per kg per K). Oops, looks like we need to know the mass of
the atmosphere. But we can figure this out, the answer is pushing right
down on our heads! We know the pressure at the surface of the Earth (1
atm = 101 kPa) and that pressure is just the result of the weight of the
atmosphere pushing down on us. Since pressure is just force / area, we
have $$ P = F/A = m_{atm}g / A_{\oplus} $$ So $$ m_{atm} =
\frac{P\times4\pi
R^2_{\oplus}}{g}=\frac{10^5\~\mbox{Pa}\times4\pi
(6\times10^6\~\mbox{m})^2}{9.8\~\mbox{m/s}^2}\approx4\times10^{18}\~\mbox{kg}.$$
Neato, gang. So we could see a temperature rise of about $$ \Delta T =
\frac{E_{ph}}{m_{atm}c_{air}}=\frac{10^{19}\~\mbox{J}}{4\times10^{18}\~\mbox{kg}\times10^3\~\mbox{J/
kg K}}\approx0.003\~\mbox{K}, $$ or three one-thousandths of a degree.
Remember, too, that this will be an upper bound since we are assuming
that all this energy is deposited into the atmosphere before it has a
chance to cool. In fact, if the energy is deposited over the course of
hours or days, this value will be much less. So it looks like we've
wrapped this thing up: Betelgeuse exploding will most certainly not put
the Earth in any danger. Or did we? We have considered the case of a
symmetric supernova, but there's more than one way to blow up a star.
Massive stars can also end their lives in a fantastic explosion called a
gamma-ray burst (GRBs to
the hep cats that study them, some fun facts relegated to [5]). GRBs are
still an intense area of current study, but the current picture (for one
type of GRB, at least) is that they are the result of a star blowing up
with the energy of the explosion focussed into two narrow beams (see
picture below). Since the flux isn't distributed over the whole sphere,
GRBs can be seen at much greater distances than a typical supernova.
 Example of a gamma-ray burst, with the explosion in two beams.
Example of a gamma-ray burst, with the explosion in two beams.
So how will this change our answer? Well, it's going to change the
fluence we calculated above. Instead of spreading the energy out over
the whole sphere, it's only going to go to some fraction of the 4pi
steradians. So we get $$ F_{ph} = \frac{E_{ph}}{4\pi f_{\Omega}
d^2}, $$ where f_{omega} is called the "beaming fraction" and tells us
what fraction of the sphere the energy goes through. Typical GRB beams
range from 1 to 10 degrees in radius. Converting this to radians, we can
find the beaming fraction as $$ f_{\Omega} = \frac{2 \times \pi
\theta^2}{4\pi} \approx
10^{-4}\left(\frac{\theta}{1^\circ}\right)^2,$$ so the beaming
fraction is 10^-4 and 10^-2 for a beam angle of 1 degree and 10
degrees, respectively. Alright, so now we can redo the calculations we
did for the supernova case, but keeping this beaming fraction around.
The total amount of energy that would hit Earth is then about
$$E_{\oplus}=\frac{E_{ph}}{4\pi f_{\Omega} d^2}\times\pi
R^2_{\oplus}\sim
10^{23}\~\mbox{J}\left(\frac{E_{ph}}{10^{44}\~\mbox{J}}\right)\left(\frac{d}{200\~\mbox{pc}}\right)^{-2}\left(\frac{\theta}{1^\circ}\right)^{-2}.$$
Holy sixth-of-a-moley! Continuing as we did above, we find that this
could potentially heat up the atmosphere by $$ \Delta T =
\frac{E_{ph}}{m_{atm}c_{air}}=\frac{10^{23}\~\mbox{J}}{4\times10^{18}\~\mbox{kg}\times10^3\~\mbox{J/
kg
K}}\approx3\~\mbox{K}\left(\frac{\theta}{1^\circ}\right)^{-2},
$$ which is certainly non-negligible. Now, this won't destroy the planet
[6], but it could make things really uncomfortable. This will be
especially true when you realize that a fair amount of the energy
carried away from a gamma-ray burst is in the form of (wait for it...)
gamma-rays, which will wreck havoc on your DNA. Remember, though, that
this is an absolute worst-case scenario since we have assumed the
smallest beaming angle. But this may still make us a little nervous, so
is there anyway to figure out if Betelgeuse could, in fact, beam a
gamma-ray burst towards Earth? Yes, yes there is. Jets and beams like
those in GRBs typically point along the rotation axis of the star [7].
If we could determine the rotational axis of Betelgeuse, then we could
say whether or not there's a chance it's pointed towards us. It just so
happens that Betelgeuse is the only star (aside from our Sun) that is
spatially resolved. If you could measure spectra along the star, you
could look for Doppler shifting of absorption lines and say something
about the velocity at the surface of the star. Luckily, this has already
been done for us (see, for example Uitenbroek et al.
1998). These
measurements are hard to do since the star is only a few pixels wide,
but it appears as though the rotation axis is inclined to the
line-of-sight by about 20 degrees (see figure below). That means this
would require a beam with at least a 20 degree radius to hit the Earth.
This appears to be outside the typical ranges observed. So even if
Betelgeuse were to explode in a gamma-ray burst, the beam would miss
Earth and hit some dumb other planet nobody cares about.
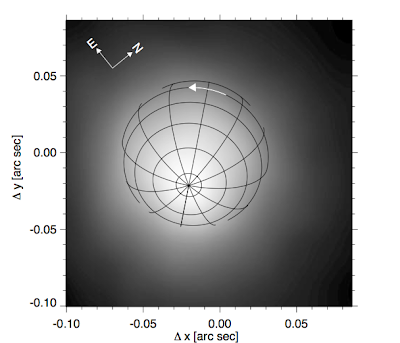 Figure reproduced from Uitenbroek et al. (1998)
Figure reproduced from Uitenbroek et al. (1998)
Alright, so the moral of the story is that Betelgeuse is completely
harmless to people on Earth. When it does explode, it will be a
brilliant supernova that would likely be visible at least a little bit
during the day. It will be the coolest thing that anyone alive (if there
are people...) will ever see. Sadly, this explosion could take place at
just about any time during the next million years. Assuming a uniform
distribution over this time period and a human lifetime of order 100
years, there is something like a 1 in 10,000 chance you'll see this in
your life. Feel free to hope for a spectacular astronomical sight, but
don't lose sleep worrying about being hurt by Betelgeuse!
Semi-excessive Footnotes: [1] This has nothing to do with the Kessel
Run. For a description of the actual distance unit see
Wikipedia. For a circuitous
retconning to correct for one throwaway line in Star Wars, see
Wookieepedia. [2] This is
how anything heavier than helium gets distributed throughout the
universe. The hydrogen and helium formed after the Big Bang gets fused
into heavier elements in stars and then dispersed out through
supernovae. In fact, most things heavier than Iron actually require
supernovae to even exist. If you have any gold on you right now (I'm
looking at you Mr. T), that only exists because a star exploded! [3]
Let's consider the case of turning 4 protons into a Helium nucleus.
Helium-4 has a binding energy
of about 28 MeV, which means that the total energy of a bound He-4
nucleus is 28 MeV less than its free protons and neutrons (in other
words, we need to put in 28 MeV to break it up). So the process of
turning 4 protons into a Helium nucleus gives off 28 MeV worth of
energy. But we had a total of 4 times 1000 MeV worth of matter we could
have turned into energy. Thus, the process was 28 MeV/4000 MeV \~ 0.7%
efficient at turning matter into energy. [4] Sometime last year, the
United States
disclosed
that its nuclear arsenal as of Sept 2009 was something like 5000
warheads. Assume these to be Megaton warheads. A Megaton is about 4
10^15 J, so the total energy in the US arsenal is about 5000 * 4
10^15 J = 2 * 10^19 J. [5] A fun fact about GRBs: They were
discovered by a military
satellite looking for
illegal nuclear tests, which would emit some gamma-rays. Instead of
seeing a signal on Earth, they saw bursts coming from space. I really
really hope that someone's first thought was that the Russians were
testing nukes on the Moon or something. We must not allow a moon-nuke
gap! [6] We here at the Virtuosi are contractually obligated to only
destroy the Earth in our posts on Earth day. I apologize for any
inconvenience this may cause. [7] I am not exactly sure why this is the
case. It is certainly observed to be the case and I thought there was a
straightforward explanation for why this was the case, but I don't
really have a good explanation. Although, maybe there just isn't a good
one yet. [8] For comparison,
there is about a 1 in 3000
chance
you'll be struck by lightning in your lifetime.
Rhubarb pie (Source: Wikipedia)







 Hi folks. It's been an embarrassingly long time since I last posted, but
today's news on the Higgs boson has brought me out of hiding. I want to
share my thoughts on today's announcement from the CMS and ATLAS
collaborations on their searches for the Higgs boson. I'm a member of
the CMS collaboration, but these are my views and don't represent those
of the collaboration. The upshot is that ATLAS sees a 2.3 sigma signal
for a Higgs boson at 126 GeV. CMS sees a 1.9 sigma excess around 124
GeV. CERN is being wishy-washy about whether or not this is actually a
discovery. After all the media hype leading up to the announcement, this
is somewhat disappointing, but maybe not too surprising. First of all,
what does a 2 sigma signal mean? The significance corresponds to the
probability of seeing a signal as large or larger than the observed one
given only background events. That is, what's the chance of seeing what
we saw if there is no Higgs boson? You can think of the significance in
terms of a Normal distribution. The probability of the observation
corresponds to the integral of the tails of the Normal distribution from
the significance to infinity. For those of you in the know, this is just
1 minus the CDF evaluated at the significance. For a 2 sigma
observation, this corresponds to about 5%. For both experiments, there
was a 5% chance of observing the signal they observed or bigger if the
Higgs boson doesn't exist. In medicine, this would be considered an
unqualified success. So why is CERN being so cagey? In particle physics
we require at least 3 sigma before we even consider something
interesting, and 5 sigma to consider it an unambiguous discovery. The
reasons why the burden of proof is so much higher in particle physics
than in other fields aren't entirely clear to me. I suspect is has to do
with the relative ease of running the collider a little longer compared
to recruiting more human test subjects, to use medicine as an example.
Given what I've just told you that we need a 3 sigma significance in
particle physics, why is everyone so excited about a couple of 2 sigma
results? Well, the first reason is that both results show bumps at
approximately the same Higgs mass. Although it's not rigorous, you can
get a rough idea of what the significance of the combined results are by
adding the significances in quadrature. This gives us about 2.8 sigma.
Higher, but still not up to the magic number of 3. The explanation for
the excitement that is most compelling brings us to Bayesian statistics.
The paradigm of Bayesian statistics says that our belief in something
given new information is the product of our prior beliefs and a term
which updates them based on the new information. Physicists have long
expected to find a Higgs boson with a mass around 120 GeV. So our prior
degree of belief is pretty high. Thus, it doesn't take as much to
convince us (or me anyway) that we have observed the Higgs boson. In
contrast, consider the OPERA collaboration's measurement of neutrinos
going faster than the speed of light. This claims to be a 6 sigma
result, but no one expected to find superluminal neutrinos, so our (or
at least my) prior for this is much lower. (Aside: If the OPERA result
is wrong, it is likely due to a systematic effect rather than a
statistical one. Nevertheless, I stand by my point.) The final thing
that excites me about this observation is that what we've seen is
completely consistent with what we would expect to see from the Standard
Model. Forgetting about significances for the moment, when the CMS
experiment fits for the Higgs boson mass, they find a cross section that
agrees very well with that predicted by the Standard Model. In the plot
below, you're interested in the masses where the black line is near 1.
The ATLAS experiment actually sees more signal than one would expect.
This is likely just a statistical fluctuation, and explains why the
ATLAS result has a higher significance.
Hi folks. It's been an embarrassingly long time since I last posted, but
today's news on the Higgs boson has brought me out of hiding. I want to
share my thoughts on today's announcement from the CMS and ATLAS
collaborations on their searches for the Higgs boson. I'm a member of
the CMS collaboration, but these are my views and don't represent those
of the collaboration. The upshot is that ATLAS sees a 2.3 sigma signal
for a Higgs boson at 126 GeV. CMS sees a 1.9 sigma excess around 124
GeV. CERN is being wishy-washy about whether or not this is actually a
discovery. After all the media hype leading up to the announcement, this
is somewhat disappointing, but maybe not too surprising. First of all,
what does a 2 sigma signal mean? The significance corresponds to the
probability of seeing a signal as large or larger than the observed one
given only background events. That is, what's the chance of seeing what
we saw if there is no Higgs boson? You can think of the significance in
terms of a Normal distribution. The probability of the observation
corresponds to the integral of the tails of the Normal distribution from
the significance to infinity. For those of you in the know, this is just
1 minus the CDF evaluated at the significance. For a 2 sigma
observation, this corresponds to about 5%. For both experiments, there
was a 5% chance of observing the signal they observed or bigger if the
Higgs boson doesn't exist. In medicine, this would be considered an
unqualified success. So why is CERN being so cagey? In particle physics
we require at least 3 sigma before we even consider something
interesting, and 5 sigma to consider it an unambiguous discovery. The
reasons why the burden of proof is so much higher in particle physics
than in other fields aren't entirely clear to me. I suspect is has to do
with the relative ease of running the collider a little longer compared
to recruiting more human test subjects, to use medicine as an example.
Given what I've just told you that we need a 3 sigma significance in
particle physics, why is everyone so excited about a couple of 2 sigma
results? Well, the first reason is that both results show bumps at
approximately the same Higgs mass. Although it's not rigorous, you can
get a rough idea of what the significance of the combined results are by
adding the significances in quadrature. This gives us about 2.8 sigma.
Higher, but still not up to the magic number of 3. The explanation for
the excitement that is most compelling brings us to Bayesian statistics.
The paradigm of Bayesian statistics says that our belief in something
given new information is the product of our prior beliefs and a term
which updates them based on the new information. Physicists have long
expected to find a Higgs boson with a mass around 120 GeV. So our prior
degree of belief is pretty high. Thus, it doesn't take as much to
convince us (or me anyway) that we have observed the Higgs boson. In
contrast, consider the OPERA collaboration's measurement of neutrinos
going faster than the speed of light. This claims to be a 6 sigma
result, but no one expected to find superluminal neutrinos, so our (or
at least my) prior for this is much lower. (Aside: If the OPERA result
is wrong, it is likely due to a systematic effect rather than a
statistical one. Nevertheless, I stand by my point.) The final thing
that excites me about this observation is that what we've seen is
completely consistent with what we would expect to see from the Standard
Model. Forgetting about significances for the moment, when the CMS
experiment fits for the Higgs boson mass, they find a cross section that
agrees very well with that predicted by the Standard Model. In the plot
below, you're interested in the masses where the black line is near 1.
The ATLAS experiment actually sees more signal than one would expect.
This is likely just a statistical fluctuation, and explains why the
ATLAS result has a higher significance. 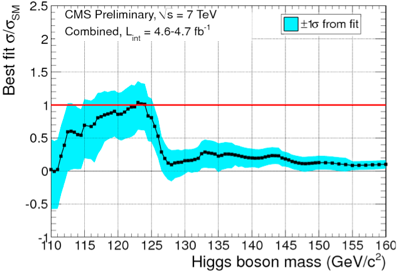
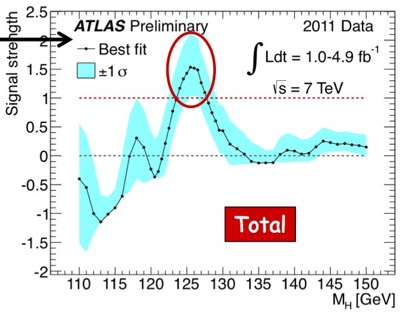 In conclusion, while CERN is being non-committal, in my opinion, we have
seen the first hints of the Higgs boson. This is mostly due to my high
personal prior that there the Higgs boson exists around the observed
mass. Unfortunately, Bayesian priors are for the most part a qualitative
thing. Thus, ATLAS and CMS are sticking to the hard numbers, which say
that what we have looks promising, but is not yet anything to get
excited about. I'll close by reminding you all to take this all with a
grain of salt. There is every possibility that this is just a
fluctuation. I'll remind you that at the end of last summer, CMS and
ATLAS both showed a
In conclusion, while CERN is being non-committal, in my opinion, we have
seen the first hints of the Higgs boson. This is mostly due to my high
personal prior that there the Higgs boson exists around the observed
mass. Unfortunately, Bayesian priors are for the most part a qualitative
thing. Thus, ATLAS and CMS are sticking to the hard numbers, which say
that what we have looks promising, but is not yet anything to get
excited about. I'll close by reminding you all to take this all with a
grain of salt. There is every possibility that this is just a
fluctuation. I'll remind you that at the end of last summer, CMS and
ATLAS both showed a 



