Last week (ok, it was a little more than a few days ago...) I used dimensional analysis to figure out how the ground's temperature changes with time. But although dimensional analysis can give us information about the length scales in the problem, it doesn't tell us what the solution looks like. From dimensional analysis, we don't even know what the solution does at large times and distances. (Although we can usually see the asymptotic behavior directly from the equation.) So let's go ahead and solve the the heat equation exactly:

$$ \frac {\partial T}{\partial t} = a \frac {\partial ^2 T}{\partial x^2} \quad (1)$$

Well, what type of solution do we want to this equation? We want the temperature at the Earth's surface $x=0$ to change with the days or the seasons. So let's start out modeling this with a sinusoidal dependence -- we'll look for a solution of the form

$$ T(x,t) = A(x)e^{i wt} $$

for some function $A(x)$, then we can take the real part for our solution. Plugging this into Eq. (1) gives $A^{\prime\prime} = i\omega/a \times A$, or

$$ A(x) = e^{ \pm \sqrt{w/2a } (1+i) x} $$

Since we have a second-order ordinary differential equation for $A$, we have two possible solutions, which are like $\exp(+x)$ or $\exp(-x)$. Which one do we choose?

Well, we want the temperature very far away from the surface of the ground to be constant, so we need the solution that decays with distance, $A\exp(-x)$. Taking the real part of this solution, we find^[1]

$$ T(x,t) = T_0 \cos (wt + \sqrt{w/2a}\times x ) e^{-\sqrt{w/2a}x} \quad (2) $$

Well, what does this solution say? As we expected from our scaling arguments last week, the distance scale depends on the square root of the time scale -- if we decrease our frequency by 4 (say, looking at changes over a season vs over a month), the ground gets cooler only $2{\times}$ deeper. We also see that the temperature oscillation drops off quite rapidly as we go deeper into the ground, and that there is a "lag" the farther you go into the ground. In particular, we see that at distances deep into the ground, the temperature drops to its average value at the surface. You can see this all in the pretty plot below (generated with Python):

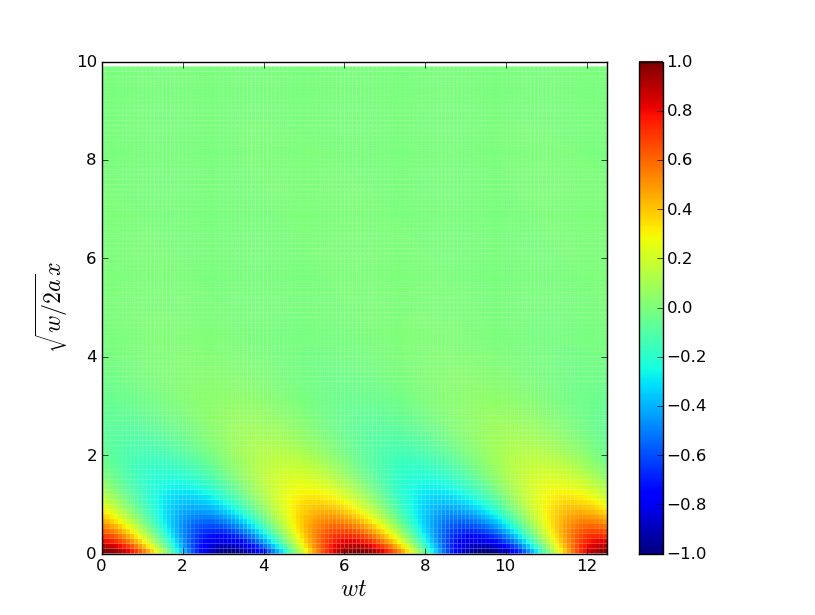
Let's recap. To model the temperature of the ground, we looked for a solution to the heat equation which had a sinusoidally oscillating temperature at $x=0$, and decayed to 0 at large $x$. We found a solution such a solution, and it shows that the temperature decays rapidly as we go far into the ground. At this point, there are two questions that pop into mind:

1) Is the solution that we found unique? Or are there other possible solutions?

2) This is all well and good, but what if our days or seasons aren't perfect sines? Can we find a solution that describes this behavior?

I'll give one (1) VirtuosiPoint to the first commenter who can prove to what extent the above solution is unique^[2]. But how about the second point? Can we solve this for non-sinusoidal time variations? Well, at this point most of the readers are rolling their eyes and shouting "Use a Fourier series and move on." So I will. Briefly, it turns out that (more or less) any periodic function can be written as a sum of sines & cosines. So we can just add a bunch of sines and cosines together and construct our final solution. So just for fun, here is a plot of the temperature of the ground in Ithaca (data from Wikipedia) over a year. (I used a discrete Fourier transform to compute the coefficients.)

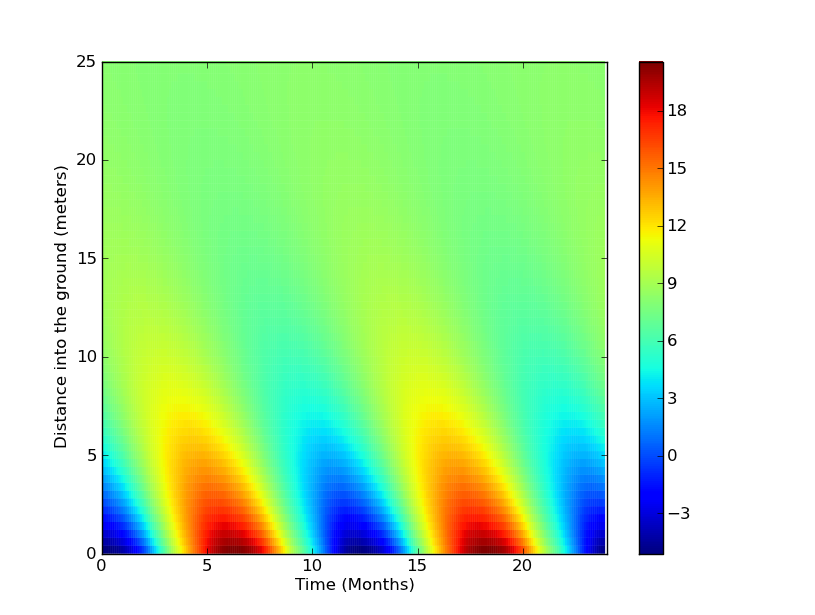
Looks pretty boring, but I swear that all the frequencies are in that plot. It just turns out that the seasons in Ithaca are pretty sinusoidal. So about 20 meters below Ithaca, the temperature is a pretty constant 8 C. While I was postponing writing this, I wondered what the temperature on Mercury's rocks would be. If we dig deep enough, can we find an area with habitable temperatures? Some quick Googlin' shows that the daytime and nighttime temperatures on Mercury are ${\sim}550-700~{\rm K}$ and ${\sim}110~{\rm K}$ at the "equator." While I don't think that Mercury's temperature varies symmetrically, let's assume so for lack of better data.^[3] Then we'd expect that deep into the surface, the temperature would be fairly constant in time, at the average of these two extremes. Plugging in the numbers (assuming $a\approx0.52~{\rm mm}^2 / s$ and using a Mercurial solar day as 176 days), we get

$T=94~{\rm C}$ at 2.75 meters into the surface.

1. ^ More precisely, since the heat equation is linear and real, if $T(x,t)$ is a solution to the equation, then so are $\frac{1}{2}(T+T^{})$ or $\frac{1}{2i}(T-T^{})$.

2. ^ Hint: It's not unique. For instance, here is another solution that satisfies the constraints, with no internal heat sources or sinks (I'll call it the "freshly buried" solution):

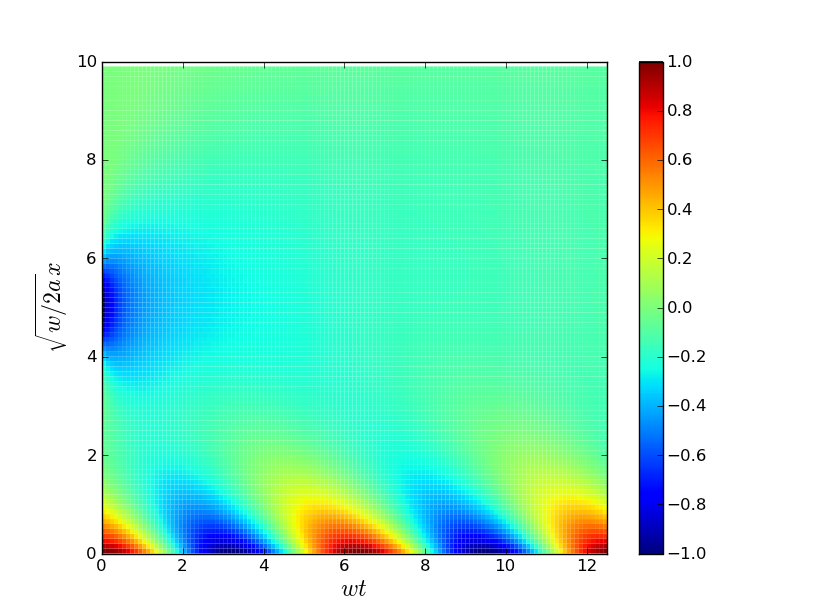
Can you prove that all the other solutions decay to the original solution? Or is there a second or even a spectrum of steady state solutions?

[3] ^ If someone provides me with better data of the time variation of Mercury's surface at some specific latitude, I'll update with a full plot of the temperature as a function of depth and time.

It snowed in Ithaca a few weeks ago. Which sucked. But fortunately, it had been warm for the previous few days, and the ground was still warm so the snow melted fast. Aside from letting me enjoy the absurd arguments against global warming that snow in April birthed, this got me thinking: How cold is the ground throughout the year? At night vs. during the day? And the corollary: How cold is my basement? If I dig a deeper basement, can I save on heating and cooling? (I'm very cheap.)

Well, we want to know the temperature distribution $T$ of the ground as a function of time $t$ and position $x$. So some googlin' or previous knowledge shows that we need to solve the heat equation.

For our purposes, we can treat the Earth as flat (I don't plan on digging a basement deep enough to see the curvature of the Earth), so we can assume the temperature only changes with the depth into the ground $x$:

$$ \frac{\partial T}{\partial t} = a \frac{\partial^2 T}{\partial x^2}\qquad (1) $$

where $a$ is the thermal diffusivity of the material, in units of square meters per second. It looks like we're going to have to solve some partial differential equations! Or will we? We can get a very good estimate of how much the temperature changes with depth just by dimensional analysis.

Let's measure our time $t$ in terms of a characteristic time of our problem $w$ (it could be 1 year if we were trying to see the change in the ground's temperature from summer to winter, or 1 day if we were looking at the change from day to night). Then we can write:

$$ \frac{\partial T }{\partial t} = \frac{1}{w} \frac {\partial T} {\partial t/w} $$

plugging this in Eq. (1), rearranging, and calling $l= \sqrt{wa}$ gives....

$$ \frac{\partial T}{\partial (t/w)} = \frac{\partial ^2 T}{\partial (x/l )^2} $$

Now let's say we didn't know how to or didn't want to solve this equation. (Don't worry, we do & we will). From rearranging this equation, we see right away there is only one "length scale" in the problem, $l$. So if we had to guess, we could guess that the ground changes temperature a distance $l$ into the ground. A quick look at Wikipedia for thermal diffusivities gives us the following table, for materials we'd find in the ground:

blloop

So we would expect that the temperature of the ground doesn't change much on a daily basis a foot or so below the ground, and doesn't change ever about 15-20 feet into the ground. Just to pat ourselves on the back for our skills at dimensional analysis, a quick check shows that permafrost penetrates 14.6 feet into the ground after 1 year. So our dimensional estimates looks pretty good! In the next few days I'll solve this equation exactly and throw up a few pretty graphs, and maybe talk a little about PDE's and Fourier series in the process.

http://tinyurl.com/7rdj996

It is traditional here at The Virtuosi to plot the destruction of the earth. We also are making secret plans for our volcano lair and death ray. However, since it is earth day, we will only share with you the plans for the total doom of the earth, not the cybernetically enhanced guard dogs we're building for our moon base. The plan I reveal today is elegant in its simplicity. I intend to alter the orbit of the earth enough to cause the earth to freeze, thus ending life as we know it. According to the internet at large, the average surface temperature of the earth is \~15 C. This average surface temperature is directly related to the power output of the sun. More precisely, it is directly related to the radiated power from the sun that the earth absorbs. Assuming that the earth's temperature is not changing (true enough for our purposes), the then power radiated by the earth must be equal to the power absorbed from the sun. More precisely $$ P_{rad,earth}=P_{abs,sun}$$ Now, the radiated power goes as $$P_{rad}=\epsilon \sigma A_{earth} T^4 $$ where A_earth is the surface area of the earth, T is the temperature of the earth, and epsilon and sigma are constants. I'll be conservative and say that I want to cool the temperature of the earth down to 0 C. The ratio of the power the earth will emit is $$\frac{P_{new}}{P_{old}}=\frac{T_{new}^4}{T_{old}^4} \approx .81$$ Note that the temperature ratio must be done in Kelvin. The power radiated by the sun (or any star) drops off as the inverse square of the distance from the sun to the point of interest: $$P_{sun} \sim \frac{1}{r^2} $$ To reduce the power the earth receives from the sun to 81% of the current value would require $$\frac{P_{sun,new}}{P_{sun,old}}=\frac{r_{old}^2}{r_{new}^2}=.81 $$ This tells us that the new earth-sun distance must be larger than the old (a good sanity check). In fact, it gives $$r_{new}=1.11 r_{old} $$ So I'll need to move the earth by 11% of the current distance from the earth to the sun. No small task! The earth is in a circular orbit (or close enough). To change to a circular orbit of larger radius requires two applications of thrust at opposite points in the orbit It turns out that the required boost in speed (the ratio of the speeds just before and after applying thrust) for the first boost of an object changing orbits is given by $$\frac{v_{f}}{v_{i}}=\sqrt{\frac{2R_{f}}{R_i+R_f}}=1.026$$ To move from the transfer orbit to the final circular orbit requires $$\frac{v_{f}}{v_{i}}=\sqrt{\frac{R_{i}+R_f}{2R_i}}=1.027$$ Note that despite the fact that we boost the velocity at both points, the velocity of the final orbit is less than that of the initial. Now, how could we apply that much thrust? Well, the change in momentum for the earth from each stage is roughly (ignoring the slight velocity increase of the transfer orbit) $$\Delta p = .03M_E v_E $$ The mass of the earth is \~610^24 kg, the orbital velocity is \~30 km/s, so $$\Delta p = 5\cdot 10^{27} kgm/s$$ A solid rocket booster (the booster rocket used for shuttle launches, when those still happened) can apply about 12 MN of force for 75 s (thank you wikipedia). That's a net momentum change of \~900 10^9 kgm/s (900 billion!). So we would only need $$\frac{2*5\cdot 10^{27}}{9\cdot 10^{11}}=12 \cdot 10^{15}$$ That's right, only 12 million billion booster rockets! With those I can freeze the earth. I assure you that this plan is proceeding on schedule, and will be ready shortly after we have constructed our volcano lair.

Five Hundred Mega Dollars, to be precise. (Image from Wikipedia)

I am not typically interested in lotteries. They seem silly and I am seriously beginning to question their usefulness in bringing about a good harvest. But this morning I read in the news that the Mega Millions lottery currently has a world record jackpot up for grabs. In fact, the jackpot is so big...

Tonight Show Audience: HOW BIG IS IT?

**

It is so big that I decided to do a little bit of analysis on the expected returns. Zing!

Some Background

First, a little background. The Mega Millions lottery is an aptly named lottery in which numbered ping pong balls are pulled from a giant rotating tub of randomization. Five of these are drawn from one tub of 56 balls, with no replacement. The sixth ball (the so-called "Mega Ball") is drawn from a separatetub of 46 balls. To play, one picks 5 different numbers (1-56) for the regular draws and one number (1-46) for the Mega Ball. The first five can match in any order, but the last ball has to match with the Mega Ball. Prizes are given out based on how many numbers you match. Stolen from the Mega Millions website, the prizes and odds are given in the table below. The current jackpot is listed at $500 million (if taken in annuity) or $359 million if taken in an up-front lump sum. It costs $1 dollar to play.

Don't worry about the asterisk. It just says CA is lame. (Source: Mega Millions)

Hot diggity daffodil, we're ready to get going!

Expected Winnings

Alright, so it costs $1 to play and we could potentially win $500 million. It sure feels like it is worth it to play (what's the harm?). But we can do better than feelings, we have... MATH!

Since we have an exhaustive list of outcomes and their probabilities (which is just the inverse of the big number in the "chances" column), we can calculate the expectation value for our winnings. The expectation value is just the sum over all the possible prize values times the probability of winning that prize. In other words,

$$\langle W \rangle = \sum_i W_i \times p_i, $$

where we denote our expected winnings in angled brackets.

In essence, this value represents the average prize you would win if you played this lottery over and over and over again (or played all the combinations of numbers).

Setting the jackpot to $500 million, we can now compute the expected winnings as

$$ \langle W \rangle = \frac{\$ 500,000,000}{175,711,536} + \frac{\$ 250,000}{3,904,701} +\frac{\$ 10,000}{689,065} + \frac{\$ 150}{15,313} + \frac{\$ 150}{13,781} $$

$$+ \frac{\$ 10}{844} + \frac{\$ 7}{306} + \frac{\$ 3}{141} + \frac{\$ 2}{75}$$

A few flicks of the abacus later, we find that the expectation value of our prize is

$$\langle W \rangle = \$ 3.02,$$

which means that after we subtract the dollar we paid for the ticket, our expected return is $2.02.

But what if we had chosen to take our winnings as a lump sum of $359 million instead of the $500 million paid out over a span of 26 years? In that case we find

$$\langle W \rangle = \$ 2.22,$$

which results in a $1.22 gain when we subtract the dollar we paid for the ticket.

At least in a statistical sense for this particular jackpot, one is better off playing than not playing. But are we forgetting anything?

The Taxman

If you win a $500 million jackpot, do you really get a $500 million jackpot? Well, no. For winnings in a lottery over $5000, the IRS withholds 25% in federal income taxes. Additionally, the winnings are subject to state taxes as well. For example, if I were to win, the great state of New York would be entitled to about 6.8% (apparently also just for winnings above $5000).

After applying federal and state taxes to the prizes above $5000, we now have an expected winnings of

$$ \langle W \rangle = \left[1-(0.25 + 0.068)\right]\times\left(\frac{\mbox{Jackpot}}{175,711,536} + \frac{\$ 250,000}{3,904,701} +\frac{\$ 10,000}{689,065}\right) $$

$$+ \frac{\$ 150}{15,313} + \frac{\$ 150}{13,781}+ \frac{\$ 10}{844} + \frac{\$ 7}{306} + \frac{\$ 3}{141} + \frac{\$ 2}{75},$$

which gives an expected net win (minus the $1 for the ticket) of $1.10 for the $500 million annuity prize and $0.55 for the $359 million up-front lump sum.

We're still in the black, but it's slowly slipping away. Is there anything else we need to factor in? Well, yes. For one thing, winning the jackpot qualifies us for the top tax bracket, so most of the winnings would be taxed at the top marginal tax rate of 35%. Welcome to the 1%, kids! [1].

Changing the federal tax rate on the jackpot from 25% to 35% and recalculating, we find net expected winnings of $0.81 for the $500 million annuity and $0.34 for the $359 million lump sum. Surprisingly, it is still worth it in a statistical sense.

Is it always like this?

One thing to keep in mind as we make these estimates is that this is a historically large jackpot. So even though it may be favorable to play this time, this will not always be the case. In fact, we can find the minimum jackpot value for which this is the case.

The condition in which our expected return is a gain (rather than a loss) is

$$ \langle W \rangle - \$1.00 > 0. $$

For simplicity, let's ignore the top marginal tax rate and just factor in the 25% withholding and the 6.8% state tax. Solving for the minimum jackpot using the expression for we found in the last section, we see that

$$ \mbox{Jackpot}_{min} = \$217\~\mbox{million}.$$

Technically, this would have to be the amount actually awarded by the payment method of your choice. The stated jackpot is always the annuity method (because it looks higher). The lump sum offering is at most about 70% of the stated jackpot. So if you want to take the lump sum offering the stated jackpot will need to be

$$ \mbox{Jackpot}_{min} = \$217\~\mbox{million} / 0.7 = \$310\~\mbox{million}.$$

In fact, these values are likely a bit low, since we have not included the increase to the marginal tax rate, nor have we included other effects like having to split a prize (which seems to happen a lot) or inflation effects if you take the prize in yearly installments.

In any case, a quick look through the jackpot history shows that these threshold values are only met occasionally. An eyeball estimate puts about one jackpot per year that exceeds the (absolute) minimum $217 million threshold.

So am I going to win?

No. No, you will not. BUT if you played record setting lotteries hundreds of millions of times, you might see decent (\~10%) returns. Although, it may just be easiest to, you know, invest that money.

Only One Useless Footnote

[1] Although, to be fair, the top marginal tax rate is currently at historical lows. It could always be worse... [back]

Let me share my worst "best idea ever" moment. Sometime during my undergraduate I thought I had solved all the world's problems. You see, on this fateful day, my hard drive was full. I hate it when my hard drive fills up, it means I have to go and get rid of some of my stuff. I hate getting rid of my stuff. But what can someone do? And then it hit me, I had the bright idea:

What if we didn't have to store things, what if we could just compute files whenever we wanted them back?

Sounds like an awesome idea, right? I know. But how could we compute our files? Well, as you may know pi is conjectured to be a normal number, meaning its digits are probably random. We also know that it is irrational, meaning pi never ends.... Since its digits are random, and they never end, in principle any sequence you could ever imagine should show up in pi eventually. In fact there is a nifty website here that will let you search for arbitrary strings (using a 5-bit format) in first 4 billion digits, for example "alemi" seems to show up at around digit 3149096356. So in principle, I could send you just an index, and a length, and you could compute the resulting file. But wait you cry, isn't computing digits of pi hard, don't people work really hard to compute pi farther and farther? Hold on I claim, first of all, I'm imagining a future where computation is cheap. Secondly, there is a really neat algorithm, the BBP algorithm, that enables you to compute the kth binary digit of pi without knowing any of the preceding digits. In other words, in principle if you wanted to know the 4 billionth digit of pi, you can compute it without having to first compute the first 4 billion other digits. Cool, this is beginning to sound like a really good idea. What's the catch? Perhaps you've already gotten a taste of it. Let's try to estimate just how far along in pi we would have to look before our message of interest shows up. Let's assume we have written our file in binary, and are computing pi in binary e.g.

1. 00100100 00111111 01101010 10001000 10000101 10100011 00001000 11010011

etc. So, if the sequence is random, there is a 1/2 chance that at any point we get the right starting bit of our file, and then a 1/2 chance we get the next one, etc. So the chance that we would create our file if we were randomly flipping coins would be $$ P = \left( \frac{1}{2} \right)^N = 2^{-N} $$ if our file was N bits long. So where do we expect this sequence to first show up in the digits of pi? Well, this turns out to be a subtle problem, but we can get a feel for it by assuming that we compute N digits of pi at a time and see if its right or not. If its not, we move on to the next group of N digits, if its right, we're done. If this were the case, we should expect to have to draw about $$ \frac{1}{P} = 2^N $$ times until we have a success, and since each trial ate up N digits, we should expect to see our file show up after about $$ N 2^N $$ digits of pi. Great, so instead of handing you the file, I could just hand you the index the file is located. But how many bits would I need to tell you that index. Well, just like we know that 10^3 takes 4 digits to express in decimal, and 6 x 10^7 takes 8 digits to express, in general it takes $$ d = \log_b x + 1 $$ digits to express a number in base b, in this case it takes $$ d = \log_2 ( N 2^N ) + 1= \log_2 2^N + \log_2 N + 1 = N + \log_2 N + 1 $$ digits to express this index in binary. And there's the rub. Instead of sending you N bits of information contained in the file, all my genius compression algorithm has manged to do is replace N bits of information in the file, with a number that takes ( \~ N + \log_2 N ) bits to express. I've actually managed to make the files larger not smaller! You may have noticed above, that even for the simple case of "alemi", all I managed to do was swap the binary message

alemi -> 0000101100001010110101001 with the index 3149096356 -> 10111011101100110110010110100100

which is longer in binary! As an aside, you may have felt uncomfortable with my estimation for how long we have to wait to see our message, and you would be right. Just because all N digits I draw at a time don't match up doesn't mean that the second half isn't useful. For instance if I was looking for 010, lets say some of the digits are 101,010. While both of those sequences didn't match, if I was looking at every digit at a time, I would have found a match. And you'd be right. Smarter people than I have computed just how long you should have to wait, and end up with the better estimation $$ \text{wait time} \sim 2^N N \log 2 $$ which is pretty darn close to our silly estimate.

There is a very fast converging algorithm for computing pi that you can do on a desktop calculator.

• Set x = 3
• Now set x = x + sin(x)
• Repeat

This converges ridiculously fast, after 1 step you get 4 digits right, after 2 steps you get 11 correct, in general we find:

# steps Digits right 1 4 2 11 3 33 4 100 5 301 6 903 7 2708 8 8124

of course on a pocket calculator, you only need to do 2 steps to have an accuracy greater than the calculator can display. To make this chart I had to trick a computer into doing high precision arithmetic, the code is here. Granted, this approximation is really cheating, since sin is a hard function to compute, and basically being able to compute sin means you know what pi is already. Really, this is just Newton's method for computing the root of sin(x) in disguise

Fun fact: pi squared is very close to 10. How close? Well, Wolfram Alpha tells me that it is only about 1% off. I first realized this fact when looking at my slide rule, pictured to the left (click to embiggen), just another reason why slide rules are awesome. It turns out I use this fact all of the time. How's that you ask? Well, I use this fast to enable me to do very quick mental arithmetic. It goes like this. For every number you come across in a calculation, drop all of the information save two parts, first, what's its order of magnitude, that is, how many digits does it have, and second, is it closest to 1, pi, or 10? The first part amounts to thinking of every number you come across as it looks in scientific notation, so a number like 2342 turns into 2.342 x 10^3, so that I've captured its magnitude in a power of 10. As for the next part, the rules I usually use are:

• If the remaining bit is between 1 and 2, make it 1
• If its between 2 and 6.5 make it pi
• if its bigger than 6.5, make it another 10

Another way to think of this is to estimate every number to be a power of ten, and then either 1, a few, or 10. The reason I choose pi is because if I use pi, I know how the rest of the arithmetic should work, namely, I only need to know a few rules, plus when I use this to estimate answers of physics formulae, making a bunch of pis show up tends to help me cancel other natural pis that are in the formulae.

$$ \pi \times \pi \sim10 \qquad \frac{1}{\pi} \sim \frac{\pi}{10} \qquad \sqrt{10} \sim \pi $$

Which you might notice is just the same approximation written in 3 different ways.

Let's work an example

$$ \begin{align} 23 \times 78 / 13 \times 2133 &= ? \ \pi \times 10 \times 100 / 10 \times \pi \times 10^3 &= ? \ \pi^2 \times 10^5 &\sim 10^6 \ \end{align}$$

of course the real answer is 294,354, so you'll notice I got the answer wrong, but I only got it wrong by a factor of 3, which is pretty good for mental arithmetic, and in particular mental arithmetic that takes no time flat.

In fact, the average error I introduce by using this approximation is just 30% or so for each number, which I've shown below [the script that produced this plot for those interested is here].

So, there you go, now you can impress all of your friends with a simple mental arithmetic that gets you within a factor of 3 or so on average.

My TV celebrates without me.

Today, as I'm sure you're aware, is Pi Day - a day for the festive consumption of pies and quiet self-reflection. In the spirit of the holiday, I'd like to present a point for discussion: Everyone has a great talent for at least one thing. That this is true for at least some people is seen through even a cursory glance at a history book: George Washington was really good at leading revolutions, Michelangelo was an outstanding ceiling painter [1], and Batman was the best at solving complex riddles (especially in English, pero especialmente en español). But I'm certain that this holds for everyone. What's your talent? Mine, as those of you who read this blog should know very well by now, is certainly not doing physics. Nope, my talent is watching TV. Seriously guys, I watch TV like a boss [2]. In light of this talent, I thought I would describe a few instances in which I have seen pi represented (for better or for worse) in TV and movies. Over the last few months, I have been re-watching a lot of the TV show Psych with my good friend and fellow Virtuosi contributor, Matt "TT" Showbiz [3]. For the uninitiated, Psych is a detective show where the main characters (Shawn and Gus) run a (fake) psychic detective agency, which allows them to solve mysteries, engage in various shenanigans, and make an inordinate number of references to Tears for Fears frontman Curt Smith [4]. In one of the episodes, Shawn and Gus enter a room where a long train of digits is written across the top of the wall. It soon becomes evident that these are the digits of pi and the camera is sure to zoom in on the famous first few digits to reassure us. But there are hundreds of digits written out and I have very little faith in TV prop people when it comes to background mathematical expressions. So I decided to check it out.

Pi on the Wall (click to enhance for texture)

Using a neat little pi searcher, I checked to see if (and where) this sequence appeared in pi. Turns out it's legit and (almost!) correct. The first 105 digits of pi (counting after the three) are:

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148

where I have underlined the 99th, 100th, and 101st digits. Looking back at the writing on the wall, we see that the 100th digit has been duplicated.

Very Almost Pi

So close! Oh well, nobody is perfect. Even though there is an error here, I very much appreciate that whoever was doing the set design decided to use the actual digits of pi. All too often I see nonsensical equations in the background of TV shows and movies when it would take exactly the same amount of work to put real equations there. So congratulations to you, O nameless prop-making intern!, for giving an accurate (well, to a part in 10^100) value of pi. Neat, so are there any other TV shows or movies that have pi in them? Well, there's Pi. Pi is film by Darren Aronofsky (Requiem for a Dream, etc) about a mathematician looking for patterns in the stock market. It's a pretty good movie with a really cool soundtrack by Clint Mansell. It also appears to display the digits of pi in the opening credits. But does it? To the Youtube-mobile! You can watch the opening credits here if you like and here is a still image of the relevant section.

Pi?

Looks pretty cool, huh? But once we get past the slick aesthetics, we see that something doesn't seem right. This number they are showing appears at first glance to be our good friend pi, but after the 8th digit the cover is blown and we see that this is actually some impostor number!

More like Darren Aron-wrong-sky.

Now, I fully understand that this has no bearing whatsoever on the film and, in the grand scheme of things, is not a Big Deal. But it would have been just as easy to put the real digits of pi here instead of just random filler. The only way that this could possibly be better than the real deal would be if it is actually a secret code. I have not yet ruled this out, as the movie is entirely about looking for meaning in seemingly random numbers. Unfortunately, the difficulty in transcribing the numbers from the screen greatly outweighs the very small chance that this isn't just gibberish. Four hundred Quatloos to anyone who can tell me if this is a code or not!

[1] And an above average Ninja Turtle to boot. [back]

[2] Yes, I am putting my TV watching skills on par with the talents of George Washington. In fact, the stoic way in which I persevered through the entirety of The Sarah Connor Chroniclesin under two weeks was described by historian David McCullough as "Washingtonian." These are simply facts. [back]

[3] The extra "T" is for extra talent. [back]

[4] A duo can absolutely have a frontman. For evidence, feel free to ask the not-George-Michael-guy from Wham! or the not-Paul-Simon-guy from Simon & Garfunkel. [back]