Five Hundred Mega Dollars, to be precise. (Image from Wikipedia)

I am not typically interested in lotteries. They seem silly and I am seriously beginning to question their usefulness in bringing about a good harvest. But this morning I read in the news that the Mega Millions lottery currently has a world record jackpot up for grabs. In fact, the jackpot is so big...

Tonight Show Audience: HOW BIG IS IT?

It is so big that I decided to do a little bit of analysis on the expected returns. Zing!

Some Background

First, a little background. The Mega Millions lottery is an aptly named lottery in which numbered ping pong balls are pulled from a giant rotating tub of randomization. Five of these are drawn from one tub of 56 balls, with no replacement. The sixth ball (the so-called "Mega Ball") is drawn from a separatetub of 46 balls. To play, one picks 5 different numbers (1-56) for the regular draws and one number (1-46) for the Mega Ball. The first five can match in any order, but the last ball has to match with the Mega Ball. Prizes are given out based on how many numbers you match. Stolen from the Mega Millions website, the prizes and odds are given in the table below. The current jackpot is listed at $500 million (if taken in annuity) or $359 million if taken in an up-front lump sum. It costs $1 dollar to play.

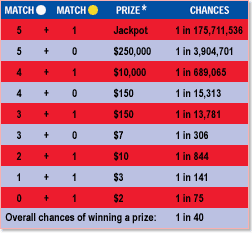Don't worry about the asterisk. It just says CA is lame. (Source: Mega Millions)

Hot diggity daffodil, we're ready to get going!

Expected Winnings

Alright, so it costs $1 to play and we could potentially win $500 million. It sure feels like it is worth it to play (what's the harm?). But we can do better than feelings, we have... MATH!

Since we have an exhaustive list of outcomes and their probabilities (which is just the inverse of the big number in the "chances" column), we can calculate the expectation value for our winnings. The expectation value is just the sum over all the possible prize values times the probability of winning that prize. In other words,

$$\langle W \rangle = \sum_i W_i \times p_i, $$

where we denote our expected winnings in angled brackets.

In essence, this value represents the average prize you would win if you played this lottery over and over and over again (or played all the combinations of numbers).

Setting the jackpot to $500 million, we can now compute the expected winnings as

$$ \langle W \rangle = \frac{\$ 500,000,000}{175,711,536} + \frac{\$ 250,000}{3,904,701} +\frac{\$ 10,000}{689,065} + \frac{\$ 150}{15,313} + \frac{\$ 150}{13,781} $$

$$+ \frac{\$ 10}{844} + \frac{\$ 7}{306} + \frac{\$ 3}{141} + \frac{\$ 2}{75}$$

A few flicks of the abacus later, we find that the expectation value of our prize is

$$\langle W \rangle = \$ 3.02,$$

which means that after we subtract the dollar we paid for the ticket, our expected return is $2.02.

But what if we had chosen to take our winnings as a lump sum of $359 million instead of the $500 million paid out over a span of 26 years? In that case we find

$$\langle W \rangle = \$ 2.22,$$

which results in a $1.22 gain when we subtract the dollar we paid for the ticket.

At least in a statistical sense for this particular jackpot, one is better off playing than not playing. But are we forgetting anything?

The Taxman

If you win a $500 million jackpot, do you really get a $500 million jackpot? Well, no. For winnings in a lottery over $5000, the IRS withholds 25% in federal income taxes. Additionally, the winnings are subject to state taxes as well. For example, if I were to win, the great state of New York would be entitled to about 6.8% (apparently also just for winnings above $5000).

After applying federal and state taxes to the prizes above $5000, we now have an expected winnings of

$$ \langle W \rangle = \left[1-(0.25 + 0.068)\right]\times\left(\frac{\mbox{Jackpot}}{175,711,536} + \frac{\$ 250,000}{3,904,701} +\frac{\$ 10,000}{689,065}\right) $$

$$+ \frac{\$ 150}{15,313} + \frac{\$ 150}{13,781}+ \frac{\$ 10}{844} + \frac{\$ 7}{306} + \frac{\$ 3}{141} + \frac{\$ 2}{75},$$

which gives an expected net win (minus the $1 for the ticket) of $1.10 for the $500 million annuity prize and $0.55 for the $359 million up-front lump sum.

We're still in the black, but it's slowly slipping away. Is there anything else we need to factor in? Well, yes. For one thing, winning the jackpot qualifies us for the top tax bracket, so most of the winnings would be taxed at the top marginal tax rate of 35%. Welcome to the 1%, kids! [1].

Changing the federal tax rate on the jackpot from 25% to 35% and recalculating, we find net expected winnings of $0.81 for the $500 million annuity and $0.34 for the $359 million lump sum. Surprisingly, it is still worth it in a statistical sense.

Is it always like this?

One thing to keep in mind as we make these estimates is that this is a historically large jackpot. So even though it may be favorable to play this time, this will not always be the case. In fact, we can find the minimum jackpot value for which this is the case.

The condition in which our expected return is a gain (rather than a loss) is

$$ \langle W \rangle - \$1.00 > 0. $$

For simplicity, let's ignore the top marginal tax rate and just factor in the 25% withholding and the 6.8% state tax. Solving for the minimum jackpot using the expression for we found in the last section, we see that

$$ \mbox{Jackpot}_{min} = \$217\~\mbox{million}.$$

Technically, this would have to be the amount actually awarded by the payment method of your choice. The stated jackpot is always the annuity method (because it looks higher). The lump sum offering is at most about 70% of the stated jackpot. So if you want to take the lump sum offering the stated jackpot will need to be

$$ \mbox{Jackpot}_{min} = \$217\~\mbox{million} / 0.7 = \$310\~\mbox{million}.$$

In fact, these values are likely a bit low, since we have not included the increase to the marginal tax rate, nor have we included other effects like having to split a prize (which seems to happen a lot) or inflation effects if you take the prize in yearly installments.

In any case, a quick look through the jackpot history shows that these threshold values are only met occasionally. An eyeball estimate puts about one jackpot per year that exceeds the (absolute) minimum $217 million threshold.

So am I going to win?

No. No, you will not. BUT if you played record setting lotteries hundreds of millions of times, you might see decent (\~10%) returns. Although, it may just be easiest to, you know, invest that money.

Only One Useless Footnote

[1] Although, to be fair, the top marginal tax rate is currently at historical lows. It could always be worse... [back]