Stirring a bowl of honey is much more difficult than stirring a bowl of water. But why? The mass density of the honey is about the same as that of water, so we aren't moving more material. If we were to write out Newton's equation, $ma$ would be about the same, but yet we still need to put in much more force. Why? And can we measure it?

The reason that honey is harder to stir is of course that the drag on our spoon depends on more than just the density of the fluid. The drag also depends on the viscosity of the fluid -- loosely speaking, how thick it is -- and the viscosity of honey is about 400 times that of water, depending on the conditions. In fact, a quick perusal of the Wikipedia article on viscosity shows that viscosities can vary by a fantastic amount -- some 13 orders of magnitude, from easy-to-move gases to thick pitch that behaves like a solid except on long time scales. The situation is even more complicated than this, as some fluids can have a viscosity that changes depending on the flow. I wanted to find a way to measure the viscosities of the stuff around me, so I made the viscometer pictured below for about $1.75 (the vending machines in Clark Hall are pretty expensive).

To do this, I

1. Enjoyed the crisp, refreshing taste of Diet Pepsi from a 20 oz bottle (come on, sponsorships).

2. Cut the top and bottom off the bottle, so all that was left was a straight tube.

3. Mounted the bottle with on top of a small piece of flat plastic.

4. Mounted a single-tubed coffee stirrer horizontally out of the bottle (I placed the end towards the middle of the bottle to avoid end effects).

5. Epoxied or glued the entire edge shut.

6. Marked evenly-spaced lines on the side of the bottle.

I can load my "sample" fluid in the top of the Pepsi bottle, and time how long it takes for the sample level to drop to a certain point. A more viscous fluid will take more time to leave the bottle, with the time directly proportional to the viscosity. (This is a consequence of Stokes flow and the equation for flow in a pipe. It will always be true, as long as my fluid is viscous enough and my apparatus isn't too big.)

So we're done! All we need to do is calibrate our viscometer with one sample, measure the times, and then we can go out and measure stuff in the world! No need to stick around for the boring calculations! We can do some fun science over the next few blog posts!

But this is a physics blog written by a bunch of grad students, so I'm assuming that a few of you want to see the details. (I won't judge you if you don't though.) If we think about the problem for a bit, we basically have flow of a liquid through a pipe (i.e. the coffee stirrer), plus a bunch of other crap which hopefully doesn't matter much.

We first need to think about how the fluid moves. We want to find the velocity of the fluid at every position. This is best cast in the language of vector calculus -- we have a (vector) velocity field $\vec{u}$ at a position $x$. There are two things we know: 1) We don't (globally) gain or lose any fluid, and 2) Newton's laws $F=ma$ hold. We can write these equations as the Navier-Stokes equations:

$$ \vec{\nabla}\cdot \vec{u} = 0 \quad (1) $$

$$ \rho \left( \frac {\partial \vec{u}} {\partial t} + (\vec{u}\cdot\vec{\nabla})\vec{u} \right) = - \vec{\nabla}p + \eta \nabla^2 \vec{u} \quad (2) $$

The first equation basically says that we don't have any fluid appearing or disappearing out of nowhere, and the second is basically $m \vec{a}=\vec{F}$, except written per unit volume. (The fluid's mass-per-unit-volume is $\rho$, the rate of change of our velocity is $\frac{d\vec{u}}{dt}$, and our force per unit volume is $\vec{\nabla}p$, plus a viscous term $\nabla^2 \vec{u}$. The only complication is that $\frac{d\vec{u}}{dt}$ is a total derivative, which we need to write as

$$ \frac{d\vec{u}}{dt} = \frac{\partial \vec{u}}{\partial t} + \frac{\partial \vec{u}}{\partial x} \frac{d x}{d t}$$

I won't drag you through the gory details, unless you want to see them, but it turns out that for my system the height of the fluid $h$ (measured from the coffee stirrer) versus time $t$ is

$$ h(t) = h(0)e^{-t/T}, \quad T= 60.7 \textrm{sec} \times [\eta / \textrm{1 mPa s}] \times [\textrm{ 1 g/cc} / \rho] $$

[For my viscometer, the coffee stirrer has length 13.34 cm and inside diameter 2.4 mm, and the Pepsi bottle has a cross-sectional area of 36.3 square centimeters (3.4 cm inner radius). You can see how the timescale scales with these properties in the gory details section.]

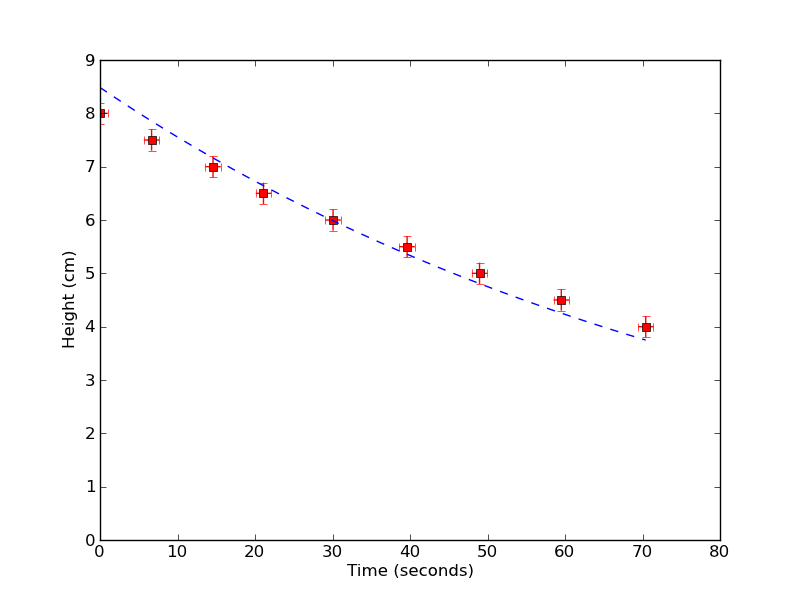
Well, how well does it work? Above is a plot of the height of water in my viscometer versus time, with a best-fit value from the equations above. To get a sense of my random errors (such as how good I am at timing the flow), I measured this curve 5 separate times. If I take into account the uncertainties in my apparatus setup as systematic errors, I find a value for my viscosity as

$$ \eta \approx 1.429 \textrm{mPa s} \pm 0.5 \% \textrm{Rand.} \pm 55\% \textrm{Syst.} $$

The actual value of the viscosity of water at room temperature (T=25 C) is about $0.86~\textrm{mPa s}$, which is more-or-less within my systematic errors. So it looks like I won't be able to measure absolute values of viscosity accurately without a more precise apparatus. But if I look at the variation of my measured viscosity, I see that I should probably be able to measure changes in viscosity to 0.5% !! That's pretty good! Hopefully over the next couple weeks I'll try to use my viscometer to measure some interesting physics in the viscosity of fluids.

A couple weeks ago, I came home after a long day at work looking for a break. I thought to myself, "What’s more fun than physics?"

Batman.^[1]

I sat down to play the latest Batman videogame, in which Batman’s current objective was to use his grappling hook to jump onto an enemy helicopter to steal an electronic MacGuffin. As awesome as this was, it occurred to me that something was very wrong about the way the helicopter moved while Batman zipped through the air.

See if you can spot it too. (Watch for about 5 seconds after the video starts. Ignore the commentary. Note: The grunting noises are the sounds that Batman makes if you shoot him with bullets.)

What occurred to me was this: If the helicopter’s rotors provided enough lift to balance the force of gravity, wouldn’t Batman’s sudden additional weight cause the helicopter to fall out of the sky? Also, to get lifted up into the air, the helicopter must be pulling up on Batman: shouldn’t Batman also be pulling down on the helicopter? By how much should we expect to see the helicopter’s altitude change?

To address the first question, let's go to Newton's second law:

$$ \sum \vec{F} = m\vec{a} $$

Let’s assume that the helicopter is hovering stationary, minding its own business, when Batman jumps onto it. Let's also assume the helicopter pilots are totally oblivious to Batman and make no flight corrections after Batman jumps onto it. In order to hover, the lift from the helicopter's rotors exactly matched the pull of gravity.

$$ \sum \vec{F} = \vec{F}{rotors} - \vec{F} = 0 $$

Batman's sudden additional weight would cause the helicopter to start falling, as the forces would no longer balance:

$$ \sum \vec{F} = \vec{F}{rotors} - \vec{F} - \vec{F}_{Batman} < 0 $$

So the helicopter does accelerate (and move) when Batman jumps onto it. How much does it move? Let’s assume there are no crazy winds or other external forces acting on the helicopter or Batman while Batman grapples onto the helicopter. “No external forces” means that momentum of helicopter + Batman does not change during Batman's flight.

Let's make things a little simpler and assume that neither Batman nor the helicopter had any vertical momentum before Batman used his grappling hook. (I can choose to approach this problem from a reference frame where the center of mass is stationary. Choosing a frame where the center of mass moves won't change the results, it will just make the calculation more complicated.) Because the momentum of helicopter + Batman does not change, then the center of mass does not move while Batman zips through the air:

$$ \frac{d}{dt} y_{COM} = \frac{d}{dt} \frac{m_{Bat} y_{Bat} + m_{Copter} y_{Copter}}{m_{Bat} + m_{Copter}} = \frac{p}{m_{Bat} + m_{Copter}} = 0 $$

The center of mass must remain stationary, so we can find how much the helicopter's height changes by if Batman starts on the ground (y = 0) and both end up at the same height with Batman hanging from the helicopter:

$$ y_{COM} = \frac{m_{Copter} y_{Copter} + m_{Bat} (0)}{m_{Bat} + m_{Copter}} = \frac{m_{Copter} y_{final} + m_{Bat} y_{final}}{m_{Bat} + m_{Copter}} $$

$$ \Delta y = y_{Copter} - y_{final} = \frac{m_{Bat}}{m_{Bat} + m_{Copter}} y_{Copter}$$

Now, some numbers: The police helicopters in the game are pretty small, probably about 1500 kg.

Batman is a big guy who works out and probably weighs around 100 kg (220 lb). Plus, he’s wearing body armor (hence surviving when bullets hit him) and a utility belt and all of those other Bat-gadgets, which probably adds about 30 kg ($\sim 30$ lb for the gadgets, $\sim30$ lb for the armor). If Batman has to grapple onto a helicopter 30 meters above him, then the helicopter should drop out of the air by about 2.4 m. This is greater than the height of Batman himself, and would be noticeable if the helicopter physics in the game were perfect. Of course, if the helicopters appearing in the game were the giant army helicopters (they do carry rockets, after all), their mass would be much larger $(\sim 5000-10000~{\rm kg})$ so the effect of Batman’s additional weight would be much smaller. None of these considerations detracted from the fun I had playing the game, but it did seem odd that the helicopters appeared to be nailed to the sky instead of moving freely through the air. I’ll be writing the game developers a strongly-worded letter directly.

Notes

1. ^ The DC superhero, not the city or the fish.

Today is the transit of Venus, which, aside from being a totally rad astronomical event, is also the perfect excuse to tell my favorite story of an unlucky Frenchman (I have many). This is by no means new and, if you've ever taken an astronomy course, you've probably already heard it. It is perhaps the closest thing Astronomy has to a ghost story, told though the glow of a flashlight on moonless nights to scare the children. This is the story of Guillaume Le Gentil, a dude that just couldn't catch a break.

Guillaume Joseph Hyacinthe Jean-Baptiste Le Gentil de la Galaisière was a Frenchman with an incredibly long name. He was also an astronomer, though he hadn't started out that way. Monsieur Le Gentil (as his friends called him and so, then, shall we) had originally intended to enter the priesthood. However, he soon began sneaking away to hear astronomy lectures and quickly switched from studies of Heaven to those heavens more readily observed in a telescope. Le Gentil happened to get into the astronomy game at a very exciting time. The next pair of Venus transits was imminent and astronomers were giddy with anticipation. Though the previous transit of 1639 had been predicted, it was met with little fanfare and only a few measurements. But the transits of 1761 and 1769 would be different. People would be ready. And the stakes were higher this time, too. Soon after the 1639 transit, Edmund Halley (he of the-only-comet-people-can-name fame) calculated that with enough simultaneous measurements, the distance from the Earth to the Sun (the so-called astronomical unit, or AU) could be measured fairly accurately. Since almost all other astronomical distances were known in terms of the AU, knowing its precise value would essentially set the scale for the cosmos. Brand new telescopes in hand, the astronomers of Europe set sail for locations all over the world.

Le Gentil had been assigned to observe the transit from Pondicherry, a French holding on the eastern side of India. On March 26th, 1760, he began his long sea voyage around the Cape of Good Hope towards India.

The voyage from France to India was a bit too long for the ship Le Gentil hitched a ride on and he only made it as far as Mauritius (a small island off Madagascar). Dropped off with all his equipment, Le Gentil was left waiting for any ship at all to take him to Pondicherry.

Perhaps it was the Curse of the Dodo or perhaps it was just bad luck, but while he was waiting, Le Gentil learned that war had broken out between the French and the British, making a trip to British India very difficult for a Frenchman.

Then the monsoon season started, meaning that even if he could find a ship, it would have to take a much longer route to India than initially planned and that it would be very difficult to make the journey before the transit occurred.

Then, he caught dysentery for the first time.

Finally, after months of waiting, Le Gentil (barely recovered from his illness) left Mauritius for India in February of 1761. Though time appeared to be running out, the captain of the ship he was on promised he would be there to observe the transit in June. About halfway to India, the winds switched directions and the ship was forced to turn back to Mauritius.

Le Gentil dutifully observed the transit of Venus in 1761 from a rocky ship in the middle of the Indian Ocean. The data were useless and he never attempted any analysis.

Although he missed the first transit, these things come in pairs separated by eight years. There was still another chance. And with all this time to prepare, there was no way he was going to miss the second one.

In fact, there was a bit too much time. But as a world-traveling 18th century man of science, Le Gentil had plenty of other interests to fill his days. He was particularly interested in surveying the region around Madagascar.

So he made a really nice map of Madagascar. And then he ate some bad kind of some kind of animal and came down with a terrible sickness. He describes this illness and its "cure" in his journals:

This sickness was a sort of violent stroke, of which several very copious blood-lettings made immediately on my arm and my foot, and emetic administered twelve hours afterwards, rid me of it quite quickly. But there remained for seven or eight days in my optic nerve a singular impression from this sickness; it was to see two objects in the place of one, beside each other; this illusion disappeared little by little as I regained my strength...

After recovering from both his sickness and the treatment, Le Gentil decided to begin his preparations for the 1769 transit of Venus. He calculated that either Manila or the Mariana Islands would be the ideal spot to observe. The Sun would be relatively high in the sky at both places when Venus passed by, meaning that the view would be through less atmosphere with a reduced chance of clouds passing through the line of sight. Le Gentil packed up his stuff and headed off to Manila, where he could catch another ship to get to the Mariana Islands. Arriving in Manila in 1766, the astronomer found himself exhausted from months of sickness and sea-voyage. So, when he was offered passage on a ship heading to the Mariana Islands, he quickly declined. That he chose not to depart Manila at that time was perhaps his one stroke of good luck in the entire journey. The ship sunk. Writing in his journal, Le Gentil appears to have developed that particular sense of humor that generally accompanies constant disappointment:

It is true that only three or four people were drowned, those who were the most eager to save themselves, which is what almost always happens in shipwrecks. I cannot answer that I would not have increased the number of persons eager to save themselves.

In any case, Le Gentil was in Manila with plenty of time to prepare for the next transit. Unfortunately, the astronomer may have over-prepared. Having arrived three years before the event, he now had three years to worry and second-guess his decision. It didn't help that the Spanish governor of Manila was kind of a crazy person. Not wanting to miss the observation of a lifetime owing to the whims of mildly insane strong man, Le Gentil packed up his stuff and headed to Pondicherry. Finally in Pondicherry, Le Gentil worked tirelessly to construct his observatory and make plenty of astronomical observations in preparation for the event. He had state of the art equipment and had fully calibrated and double checked everything. It was now nine years since his journey began and only a few days until the transit was scheduled to occur at sunrise on June 4th. The entire month of May was beautiful weather and pristine observing conditions, as were the first few days of June. Le Gentil likely went to bed on the 3rd of June fully confident that the next morning would be no different. He woke up early in the morning to begin preparations for his sunrise observations only to find clouds on the horizon. The clouds remained, obscuring the sun, all through the duration of the transit. A few hours after the end of the transit, the sun broke through the clouds and remained visible for the rest of the day. Le Gentil had missed his second transit in Pondicherry. He sums it up in his journal:

That is the fate which often awaits astronomers. I had gone more than ten thousand leagues; it seemed that I had crossed such a great expanse of seas, exiling myself from my native land, only to be the spectator of a fatal cloud which came to place itself before the sun at the precise moment of my observation, to carry off from me the fruits of my pains and of my fatigues

In Manila, the Sun rose in perfectly clear skies. Distraught, Le Gentil remained in bed for some weeks afterward. He soon caught a fever and missed the ship that was supposed to take him home. He recovered, but then came down with dysentery again. Barely recovered from his various illnesses, he managed to get a ride back to Mauritius. He caught a ship leaving the island in November of 1770. The ship was struck by a hurricane and almost completely destroyed. It managed to limp back to Mauritius. The second attempt proved more successful and Le Gentil finally "set foot on France at nine o'clock in the morning, after eleven years, six months and thirteen days of absence." Though he had finally made it home, he was not out of the woods quite yet. In his absence, Le Gentil's heirs had tried to declare him dead to gain their inheritance, his accountant had mishandled (and lost) a large chunk of his holdings, and the Academy of Sciences, which had sent him on his 11 year mission, had given his seat to someone else. It was not quite the welcome home he had hoped for. Despite his seemingly never-ending misfortune, things did turn around for Le Gentil. He married, had a daughter, and was reinstated into the Academy of Sciences. Presumably, he lived out the rest of his days in relative happiness. Le Gentil died in 1792. Keeping true to his style, this man who missed two of the most important astronomical events of his time fortunately managed to also miss the most important (and violent) political event of his time.

References:

I have mainly used a very nice series of historical papers of Le Gentil's misadventures with the transit of Venus written by Helen Sawyer Hogg. The papers were originally published in the Journal of the Royal Astronomical Society of Canada and can be accessed through NASA's ADS (Part 1, Part2, Part 3, Part 4).

More Transit of Venus:

If you want to see the Transit of Venus without having to go on an eleven year voyage (or even leaving your room), check out the NASA live-feed from Mauna Kea.