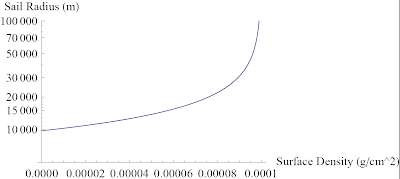
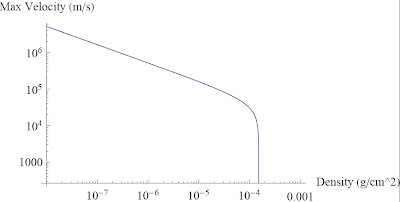
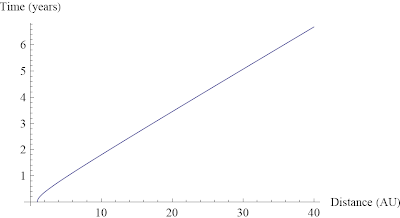
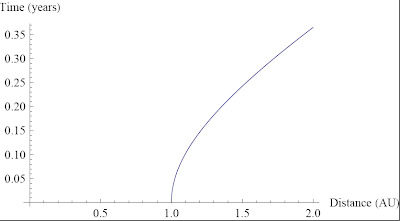
Ask a Physicist: Volume I
We
have received our first Ask a Physicist e-query! An entity known only
to us as "Hungry" writes:
"We had a dispute at a dinner party about whether blowing on hot food
actually makes it cool down faster, or only gives you something to do
while you wait for your food to cool."
While it is questionable whether or not I am indeed a physicist (but
people do pay me to do physics) and whether I will answer definitively
(there'll be some hand-waving), I'll give it my darndest.
Let's imagine a hot baked potato you just sliced open. The mass of
potato is capable of transferring energy as heat to the surrounding air
(and therefore cooling down) via a number of mechanisms. The most common
we hear about are conduction, radiation, and convection. Conduction is
the process by which two objects in intimate contact exchange heat.
Radiation is a bit more mysterious, but in the same way that a poker in
the fire can glow white hot, all things at non-zero temperature emit
electromagnetic radiation, which carries away energy from your potato.
Convection is even more complicated, but is one of the most important
processes by which solids exchange heat with gases. Convection in our
case occurs when the potato heats up the gas at its surface. The random
motion of air molecules (now a little hotter) will "randomly" dissipate
heat. However, the hotter gas is less dense than the room temperature
gas, and buoyant forces (think Helium balloon) will create a current of
hot gas upwards from the potato surface. Both of these processes
constitute convection.
Convection is REALLY hard to describe with physical models. You can do
some computer simulations of the motion of the gas in convection. I
found this cool picture on Wikipedia of someone who did just that:
 Pretty cool. Now! To actually answer your question. To get a qualitative
answer, we don't even need to consider models of convection, etc. Isaac
Newton was kind enough to find an empirical relation for the process of
cooling, aptly named "Newton's law of cooling". If we call the amount of
heat transferred from the potato Q, the found that the rate of heat
being lost by the potato is proportional to the temperature difference
between the surrounding gas and the potato itself:
$$ \text{Rate of Heat Loss}=\frac{\text{Amount of Heat
Loss}}{\text{Amount of time}}=\frac{\Delta Q}{\Delta t} \propto
T_{\text{Potato}}-T_{\text{Air }} $$ So the quantity which is of
primary importance is the temperature difference between your potato and
the surrounding air. Now we can answer the question. If you let your
potato cool down naturally, then the potato heats the air which then
starts to convect. This means that the air immediately above the potato
is quite hot. If you blow on the potato, however, you get the air
circulating faster than it would by convection alone, effectively
replacing the hot air with slightly cooler air. And since the cooling
rate is proportional to to temperature difference; this will result in a
faster cooling rate. To first order, blowing on your food should help.
So, Hungry, feel free to blow on your food, Miss Manners be damned.
Pretty cool. Now! To actually answer your question. To get a qualitative
answer, we don't even need to consider models of convection, etc. Isaac
Newton was kind enough to find an empirical relation for the process of
cooling, aptly named "Newton's law of cooling". If we call the amount of
heat transferred from the potato Q, the found that the rate of heat
being lost by the potato is proportional to the temperature difference
between the surrounding gas and the potato itself:
$$ \text{Rate of Heat Loss}=\frac{\text{Amount of Heat
Loss}}{\text{Amount of time}}=\frac{\Delta Q}{\Delta t} \propto
T_{\text{Potato}}-T_{\text{Air }} $$ So the quantity which is of
primary importance is the temperature difference between your potato and
the surrounding air. Now we can answer the question. If you let your
potato cool down naturally, then the potato heats the air which then
starts to convect. This means that the air immediately above the potato
is quite hot. If you blow on the potato, however, you get the air
circulating faster than it would by convection alone, effectively
replacing the hot air with slightly cooler air. And since the cooling
rate is proportional to to temperature difference; this will result in a
faster cooling rate. To first order, blowing on your food should help.
So, Hungry, feel free to blow on your food, Miss Manners be damned.