Solar Sails I
 Solar sails are in the news again, and this time not just for blowing
up.
The Japanese space agency is
launching
what they hope to be the first successful solar sail tomorrow. In honor
of that, we will be discussing the physics of solar sails.
First of all, what the heck are solar sails? Solar sails are a means of
propulsion based on the simple observation that "Hey, sails work on
boats. Therefore, they should work on interplanetary spacecraft (in
space)." Boat sails work when air molecules hit into the sail and bounce
back. By conservation of momentum, this gives the boat sail an itty
bitty boost in momentum. Summing over the large number of air molecules
moving as wind, the boat gets pushed along in the water. A similar
process works with solar sails, but instead of air molecules doing the
hitting, it's photons. Since each photon of a given wavelength has some
momentum, by reflecting that photon the solar sail can gain a tiny bit
of momentum. Summing over the large number of photons coming from the
sun over a long time frame we can get a considerable boost. So let's see
how good solar sails are.
First we need to find the net force on our sail. We will certainly have
to deal with gravitational forces (which will slow us down) :
$$ F_{g} = \frac{-GM_{\odot}m}{r^2} $$
where big M is the mass of the sun and little m is the mass of the sail.
Now we need to find the radiation force on the sail. Since force is just
rate of change of momentum, we can find the change of momentum of one
photon per unit time, then find how many photons are hitting our sail.
So for one elastic collision of a photon with the sail, the change in
momentum will be
$$ \Delta p = 2 \frac{h\nu}{c} $$
and by conservation of momentum, this will also be the momentum gained
by the sail. Now we want to find the number of photons incident on a
given area in a given time. This will just be the energy flux output by
the sun ( energy/ m^2 s ) divided by the energy per photon. In other
words:
$$ f_n = \frac{L_{\odot}}{4\pi r^2}\frac{1}{h\nu} .$$
So now we can get a force by
$$ \text{Force} = \left(\frac{\Delta p}{\text{1 photon}} \right)
\times \left(\frac{\text{number of photons}}{area \times
time}\right) \times \left( Area\right) $$
which is just
$$ F_{rad} = 2 \frac{h\nu}{c} \times \frac{L_\odot}{4\pi r^2
h\nu} \times \pi R^2 = \frac{L_{\odot} R^2}{2cr^2} .$$
So combining the radiation force with the gravitation force, we have a
net force on the sail of
$$ F = \left( \frac{L_{\odot} R^2}{2c} - GM_{\odot}m \right)
\frac{1}{r^2} .$$
This can then be integrated over r to find an effective potential,
giving:
$$ U = \left( \frac{L_{\odot} R^2}{2c} -
GM_{\odot}m\right)\frac{1}{r} .$$
For simplicity, let's just write that
$$ \alpha = \frac{L_{\odot} R^2}{2c} - GM_{\odot}m $$
so
$$ U = \frac{\alpha}{r} .$$
Now we can start saying some things about this sail. The most
straightforward quantity to find would be the maximum velocity. By
conservation of energy (and starting from some r_0 at rest), we have
that
$$ v_f = \left[\frac{2\alpha}{m} \left(\frac{1}{r_0} -
\frac{1}{r_f} \right) \right]^{1/2} $$
So as r_f goes to very large values, the subtracted piece gets smaller
and smaller. In the limit that r_f goes to infinity we have that
$$ v_{max} = \left(\frac{2\alpha}{mr_0}\right)^{1/2} .$$
Plugging back in our long term for alpha and plugging in some numbers we
get:
$$ v_{max} = 42,000 m/s \left( \frac{1.5 \times 10^{-4}}{\sigma} -
1\right)^{1/2} $$
where sigma is just the surface mass density [g/cm^2] of the sail.
Below is a plot of maximum velocity ( m/s) plotted against surface mass
density (g/cm^2). For a sigma of 10^-4 g/cm^2, we get a max velocity
of about 30,000 m/s. Not bad.
Solar sails are in the news again, and this time not just for blowing
up.
The Japanese space agency is
launching
what they hope to be the first successful solar sail tomorrow. In honor
of that, we will be discussing the physics of solar sails.
First of all, what the heck are solar sails? Solar sails are a means of
propulsion based on the simple observation that "Hey, sails work on
boats. Therefore, they should work on interplanetary spacecraft (in
space)." Boat sails work when air molecules hit into the sail and bounce
back. By conservation of momentum, this gives the boat sail an itty
bitty boost in momentum. Summing over the large number of air molecules
moving as wind, the boat gets pushed along in the water. A similar
process works with solar sails, but instead of air molecules doing the
hitting, it's photons. Since each photon of a given wavelength has some
momentum, by reflecting that photon the solar sail can gain a tiny bit
of momentum. Summing over the large number of photons coming from the
sun over a long time frame we can get a considerable boost. So let's see
how good solar sails are.
First we need to find the net force on our sail. We will certainly have
to deal with gravitational forces (which will slow us down) :
$$ F_{g} = \frac{-GM_{\odot}m}{r^2} $$
where big M is the mass of the sun and little m is the mass of the sail.
Now we need to find the radiation force on the sail. Since force is just
rate of change of momentum, we can find the change of momentum of one
photon per unit time, then find how many photons are hitting our sail.
So for one elastic collision of a photon with the sail, the change in
momentum will be
$$ \Delta p = 2 \frac{h\nu}{c} $$
and by conservation of momentum, this will also be the momentum gained
by the sail. Now we want to find the number of photons incident on a
given area in a given time. This will just be the energy flux output by
the sun ( energy/ m^2 s ) divided by the energy per photon. In other
words:
$$ f_n = \frac{L_{\odot}}{4\pi r^2}\frac{1}{h\nu} .$$
So now we can get a force by
$$ \text{Force} = \left(\frac{\Delta p}{\text{1 photon}} \right)
\times \left(\frac{\text{number of photons}}{area \times
time}\right) \times \left( Area\right) $$
which is just
$$ F_{rad} = 2 \frac{h\nu}{c} \times \frac{L_\odot}{4\pi r^2
h\nu} \times \pi R^2 = \frac{L_{\odot} R^2}{2cr^2} .$$
So combining the radiation force with the gravitation force, we have a
net force on the sail of
$$ F = \left( \frac{L_{\odot} R^2}{2c} - GM_{\odot}m \right)
\frac{1}{r^2} .$$
This can then be integrated over r to find an effective potential,
giving:
$$ U = \left( \frac{L_{\odot} R^2}{2c} -
GM_{\odot}m\right)\frac{1}{r} .$$
For simplicity, let's just write that
$$ \alpha = \frac{L_{\odot} R^2}{2c} - GM_{\odot}m $$
so
$$ U = \frac{\alpha}{r} .$$
Now we can start saying some things about this sail. The most
straightforward quantity to find would be the maximum velocity. By
conservation of energy (and starting from some r_0 at rest), we have
that
$$ v_f = \left[\frac{2\alpha}{m} \left(\frac{1}{r_0} -
\frac{1}{r_f} \right) \right]^{1/2} $$
So as r_f goes to very large values, the subtracted piece gets smaller
and smaller. In the limit that r_f goes to infinity we have that
$$ v_{max} = \left(\frac{2\alpha}{mr_0}\right)^{1/2} .$$
Plugging back in our long term for alpha and plugging in some numbers we
get:
$$ v_{max} = 42,000 m/s \left( \frac{1.5 \times 10^{-4}}{\sigma} -
1\right)^{1/2} $$
where sigma is just the surface mass density [g/cm^2] of the sail.
Below is a plot of maximum velocity ( m/s) plotted against surface mass
density (g/cm^2). For a sigma of 10^-4 g/cm^2, we get a max velocity
of about 30,000 m/s. Not bad.
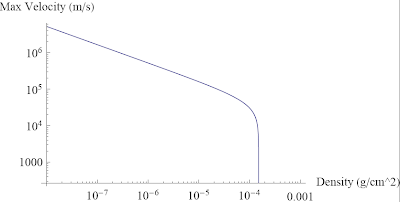 From this graph we see that there must be some maximum surface density,
above which we don't get any (forward) motion at all. This makes sense
since we want our radiation forces (which scale with area) to overcome
our gravitational forces (which scale with mass). And below this maximal
surface density we see a power law behavior. Cool.
We can also find the distance traveled as a function of time. Taking the
final velocity equation above and writing v as dr/dt, we see that
$$ \frac{dr}{dt} = \left[ \frac{2\alpha}{m} \left( \frac{1}{r_0}
- \frac{1}{r_f} \right)\right]^{1/2} $$
Rearranging and integrating, we can get time (in years) as a function of
distance r (in AU):
$$ t = \frac{0.11 \left(\sqrt{(-1+r)
r}+\text{Log}\left[1+\sqrt{\frac{-1+r}{r}}\right]+\frac{\text{Log}[r]}{2}\right)}{\sqrt{-1+\frac{1.5
\times 10^{-4}}{\sigma}}}$$
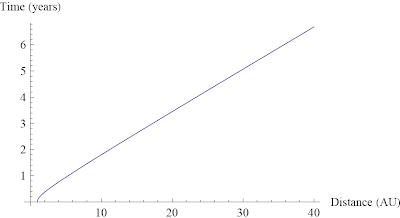
A plot of t vs. r is shown below for typical solar system distances and
a sigma of 10^-4 g/cm^2. We assume that we are launching from earth (1
AU). Since Pluto is at a distance of about 40 AU, we see that our sail
could get there in less than 7 years. For comparison, the New
Horizons probe will use conventional
propulsion to get to Pluto in 9.5 years (and it is the fastest
spacecraft ever made).
From this graph we see that there must be some maximum surface density,
above which we don't get any (forward) motion at all. This makes sense
since we want our radiation forces (which scale with area) to overcome
our gravitational forces (which scale with mass). And below this maximal
surface density we see a power law behavior. Cool.
We can also find the distance traveled as a function of time. Taking the
final velocity equation above and writing v as dr/dt, we see that
$$ \frac{dr}{dt} = \left[ \frac{2\alpha}{m} \left( \frac{1}{r_0}
- \frac{1}{r_f} \right)\right]^{1/2} $$
Rearranging and integrating, we can get time (in years) as a function of
distance r (in AU):
$$ t = \frac{0.11 \left(\sqrt{(-1+r)
r}+\text{Log}\left[1+\sqrt{\frac{-1+r}{r}}\right]+\frac{\text{Log}[r]}{2}\right)}{\sqrt{-1+\frac{1.5
\times 10^{-4}}{\sigma}}}$$
A plot of t vs. r is shown below for typical solar system distances and
a sigma of 10^-4 g/cm^2. We assume that we are launching from earth (1
AU). Since Pluto is at a distance of about 40 AU, we see that our sail
could get there in less than 7 years. For comparison, the New
Horizons probe will use conventional
propulsion to get to Pluto in 9.5 years (and it is the fastest
spacecraft ever made).
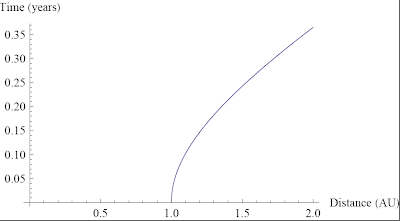
 Zooming in to our starting point around 1 AU, we see that there is a
period of acceleration and then the maximum velocity is reached after a
few months. Just eyeballing it, it looks like it takes at least a month
to reach appreciable speed. That it takes so long is a result of the
very small forces involved due to radiation pressure. But even a small
acceleration amounts to a considerable speed if applied for long enough!
Zooming in to our starting point around 1 AU, we see that there is a
period of acceleration and then the maximum velocity is reached after a
few months. Just eyeballing it, it looks like it takes at least a month
to reach appreciable speed. That it takes so long is a result of the
very small forces involved due to radiation pressure. But even a small
acceleration amounts to a considerable speed if applied for long enough!
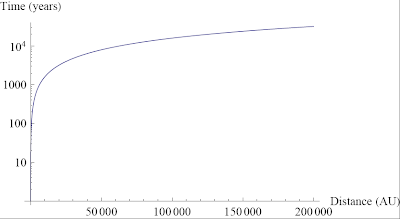
 Now Pluto is fine I guess (it's the second largest dwarf-planet!), but
how about some interstellar flight? Well, the nearest star is Proxima
Centauri which is about a parsec away. A parsec is 310^16 m, or about
200,000 AU. From, the plot below (or plugging in to the equation above),
we see that such a trip would take of order 10,000 years. That's a long
time, but its not too shabby considering this craft uses no fuel of its
own.
Now Pluto is fine I guess (it's the second largest dwarf-planet!), but
how about some interstellar flight? Well, the nearest star is Proxima
Centauri which is about a parsec away. A parsec is 310^16 m, or about
200,000 AU. From, the plot below (or plugging in to the equation above),
we see that such a trip would take of order 10,000 years. That's a long
time, but its not too shabby considering this craft uses no fuel of its
own.
 So solar sails can do some fairly impressive things simply by harnessing
the free energy of the sun. Though this only provides a very small
acceleration, it can be taken over a long enough time to be useful.
However, since the radiation pressure of the sun falls off as 1/r^2, we
start to observe diminishing returns and the sail reaches a max
velocity. But overall the numbers seem fairly impressive. All that
remains now is whether they are feasible to construct. Right now my only
data point for feasibility was that it was in Star
Wars, but as I
recall that was a long* time ago.
So solar sails can do some fairly impressive things simply by harnessing
the free energy of the sun. Though this only provides a very small
acceleration, it can be taken over a long enough time to be useful.
However, since the radiation pressure of the sun falls off as 1/r^2, we
start to observe diminishing returns and the sail reaches a max
velocity. But overall the numbers seem fairly impressive. All that
remains now is whether they are feasible to construct. Right now my only
data point for feasibility was that it was in Star
Wars, but as I
recall that was a long* time ago.
Comments
Comments powered by Disqus