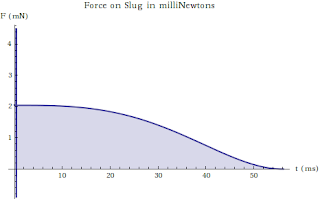
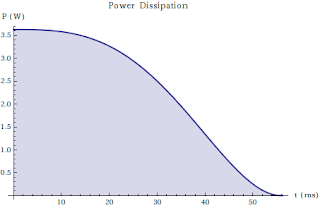
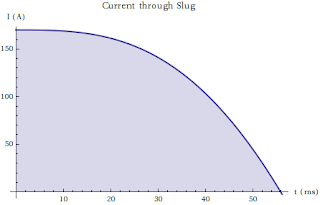
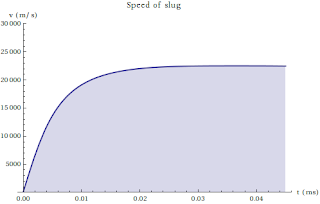
On the Nature of Many Penny Systems
The other day I was on my way through ye olde internets to the Quantum Leap episode index at Wikipedia, but stumbled over a quote by Feynman by accident: "There are 10^11 stars in the galaxy. That used to be a huge number. But it's only a hundred billion. It's less than the national deficit! We used to call them astronomical numbers. Now we should call them economical numbers" So this got me thinking. What if we decided to pay the national debt...in pennies? Seems fair enough, we don't really want to pay it and when you don't want to pay something but you have to you pay it in pennies. Hooray! Last I heard this figure was somewhere around $10,000,000,000,000 (ten trillion), that is: $$ \text{Debt} = 10^{13} \text{dollars} = 10^{15} \text{pennies} $$ Given that a penny is about 1.5 mm thick, how far does stacking them end to end take us? Well: $$ \text{Length} = (10^{15} \text{pennies}) \times ( 0.15 \text{cm}) = 1.5 \times 10^{14} \text{cm} $$ As a bit of comparison, the mean distance from the earth to the sun is $$ \text{a} = 1.5 \times 10^{13} \text{cm,} $$ so our penny stack goes out to 10 AU, which just barely passes by Saturn. Impressive! Fine, so we've got all our pennies out now and we want to fit them in a more economical fashion, taking advantage of all three of our dimensions. How big is the warehouse needed to hold all these shiny Lincolns? Well, we know (or can guess) that one penny weighs about a gram (technically 2.5 g). So if we were to know the density of a penny, we would be good to go. A good guess at density for any metal is around 10 g /cm^3 , and this is true for zinc ( FUN FACT: Pennies were almost entirely made of copper up until 1982, when they switched to 97.5% zinc, 2.5% copper). So, $$ \text{Mass} = (10^{15} \text{pennies}) \times ( 1 \frac{ \text{g}}{\text{penny}})= 10^{15} \text{g} $$ $$ \text{Volume} = \frac{\text{mass}}{\text{density}} = \frac{10^{15}\text{g}}{10 \frac{\text{g}}{\text{cm}^{3}}} = 10^{14} \text{cm}^{3}= 0.1 \text{km}}^{3} $$ That's a warehouse 1 km wide, 1km long, and a 100 m high. Pretty big. So our next logical progression would be to ask: what are its gravitational properties? To do this let's stack our pennies in a sphere. In that case we have $$ \text{Volume} = \frac{4 \pi}{3} \text{R}^{3} $$ so $$ \text{R} = (\frac{3}{4 \pi} \text{Volume})^{1/3} = (\frac{3}{4 \pi} 10^{14} \text{cm}^{3})^{1/3} \approx 3 \times 10^4 \text{cm}=0.3 \text{km.} $$ To find the gravitational binding energy of a sphere of uniform density we use $$ \text{Binding Energy} = \frac{3}{5} \frac{\text{G}\text{M}^{2}}{R}\text{.} $$ So $$ \text{Binding Energy} = \frac{3}{5} \frac{ (7 \times 10^{-8} \frac{cm^3}{gs^2})(10^{15} \text{g})^{2}}{3 \times 10^{4} \text{cm}} \approx 10^{18} \text{ergs} = 10^{11} \text{Joules.} $$ Noting that the useful measure of destruction, the kiloton of TNT, is about 10^12 J, we see that the binding energy of our spherical mass of pennies is about 100 tons of TNT. So what does this mean to us practically? Well, the binding energy of an object essentially tells us how much energy we need to put in to completely break up the body. So to fully disperse our pennies off to our lendors, we need about 100 tons of TNT worth of energy. An alternative financial fermi problem that might be interesting is how many trees would it take to make the money to equal the national debt or GDP?