This photo has been making the rounds on the internet lately:

Originally from here. Its
a time lapse photo of the sun taken from a pinhole camera from June
until December. The real question is: Where was this photo taken?
Wandering Sun
Well, first lets think a second about why the sun would wander in the
sky. As you may already know, the earth's pole is not aligned with our
solar system's axis. The earth's axis has what is called a 23.5 degree
axial tilt, or obliquity.
As a result, if you sit at a fixed latitude on the earth, then as the
earth revolves around the sun and the year goes by, the angle the sun
makes with the horizon changes. We need to estimate how much the sun's
angle in the sky changes. Consider the following diagram
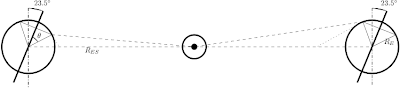
You'll notice that the angle that the dashed line towards the sun makes
with respect to the dotted horizon line, changes when the earth is on
either side of the sun. But how much does it change? We can estimate it
by realizing that the angle of that triangle centered at the sun is very
small. Very small indeed. We could estimate its size by: $$ \arctan
\frac{R_{\text{Earth}}}{D_{\text{Earth-Sun}}} \approx
0.002^{\circ} $$ Very small. So, knowing that the one angle is very
tiny, and remembering that the sum of all of the angles in a triangle
must add up to 180 degrees, we can calculate how much that angle in the
sky changes. Notice that the angle between the line pointing to our
latitude of interest and the equator has a known angle, namely the angle
there is our latitude +/- 23.5 degrees. So if that is the angle our
observation point makes with the horizontal, by the reasoning above, the
angle that the sun makes with respect to our observation point ought to
be 180 - our latitude +/- 23.5 degrees. So on either side of the sun,
the difference in this angle from summer to winter is just twice 23.5
degrees of 47 degrees. So, regardless of where you are on the earth,
between when the sun is highest in the sky, and when it is lowest in the
sky, there ought to be a 47 degree difference. (Assuming of course you
can see the sun year round, which you can't if you live too far north).
Great. So we know that the difference between the height of the traces
in the picture and the bottom needs to be 47 degrees. But that still
doesn't help us calculate the latitude the picture was taken at.
Finding Latitude in theory
Looking at our diagram again, we notice that when the sun is lowest in
the sky, we can calculate directly what angle the sun should make with
respect to the horizon (psi) (We already obtained the upper angle in our
triangle, the last part is realizing that the angle to the horizon from
the radial line is just 90 degrees). We obtain $$ \psi = \theta -
90^\circ + 23.5^\circ = \theta + 66.5^\circ $$ So, turning it on
its head, we can calculate the latitude (theta) we are at if we know the
lowest angle the sun makes in the sky $$ \theta = 66.5^\circ - \psi
$$ Great.
Finding Latitude in Practice
So, now I know two things. The total angle difference between the upper
most the sun gets and the lowest point in the sky is 47 degrees. And I
also know that if I know the angle between the horizon and the lowest
point the sun gets in the sky, I can calculate the latitude. So how am I
going to do this, well, I just took the picture and opened it up in
Gimp, and used the measure tool to get the difference between the
highest and lowest points in the sky in pixels, and the distance to the
horizon in pixels. Here's one example of my guesses:

Getting the differences in height for the sun was relatively straight
forward. In order to get the distance to the horizon, I had to guess a
little bit. I just lined it up by eye to where I thought the horizon
should be in the picture since its not visible. Why does this do me any
good? Well assuming the picture doesn't have too much distortion, since
I know the one angle is 47 degrees, I can make a comparison between the
pixel lengths. Lets say in the picture above I call the length of the
green line B, and the length of the yellow line S, then I can estimate
$$ \frac{\psi}{S} = \frac{47^\circ}{B} $$ which gives me a measure
on psi. Since I was doing this by eye, I repeated the measurement ten
times independently for each, obtaining in the end $$ B = 356 \pm 2
\qquad S = 66 \pm 6 $$ And I have a complete formula for my estimation
of the latitude $$ \theta = 66.5^\circ - 47^\circ \frac{S}{B} $$
Results
This allowed me to estimate the latitude at 58 +/- 1 degree latitude.
Naturally, I can't tell the difference between 58 degrees north or 58
degrees south. To get a better idea of what this guess looks like, here
I've overlayed the possible locations in green
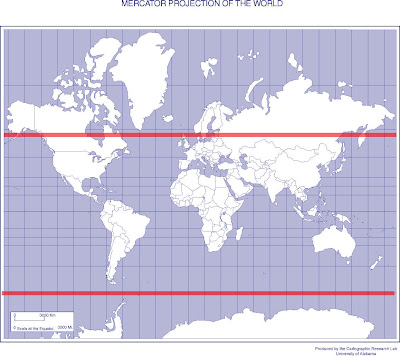
You'll notice that there isn't much life down at 58 degrees south of the
equator. So, I reckon the picture was taken in the northern hemisphere.
Surfing around on the webpage where the picture was found, you'll first
notice that its taken from a co.uk site (Great Britain), and if you go
to the homepage, Mr. Mallon has a weather widget which says Bellshill.
Google
Maps
tells me that Bellshill, UK is at about 56 degrees North. I've tried to
put a green dot on the map above near where Bellshill actually is (its
hard to see). Not bad for a night's work.







