Breaking Intuition

When I walked into my first day of physics class in high school, I carried with me a set of ideas which I learned from simply observing and interacting with the world. In fact everyone builds up what they believe to be intuitive concepts, whether it be in science, math, or any other field. Without any scientific training whatsoever, we begin to build intuition. If you let go of a ball in the air, what will happen? If you try to run on the ice of a frozen lake, will it be easier than running on the sidewalk? If you stand in the sun and on the ground you see a strange dark misshapen copy of yourself imitating your every move... who is following you? Unfortunately we run into an issue when our intuition disagrees with experimental results or someone else’s intuition. At that point, it is essential to break down and analyze our intuition to find where any problems in our logic may exist. This process of continually breaking down and analyzing intuition is key to progressing in science. Let's take a look at a simple dice game. The rules of the game dictate that you pick a die first, then I pick a die, then we roll together 100 times (we’re really bored, apparently). The winner is the person who rolls a higher number more times in 100 rolls. The catch is that the numbers are not the standard 1-6 on each die, but a magic set of numbers which may repeat any number from 1-6 as many times as desired, for example {1, 2, 3, 4, 5, 5}. "Sounds easy," you say, as you pick up the yellow die. I choose blue. We roll, and I win 74 out of 100 times. "Obviously the blue die is better, give me that one," you say. I proceed to pick up the green die, lo and behold, I win 63 out of 100 times. "Okay okay, I've got the hang of it now. Clearly the green die is better than all of the rest." I choose the yellow die and win 65 out of 100 times. In a fit of rage you proclaim "witchcraft" and storm off for your witch-hunt gear. There is no deception here with the exception of logic, the younger sister of witchcraft. It is actually an interesting challenge to try to come up with a set of numbers which will yield the following result: The probability of the value on the blue die being higher than the value on the yellow die is greater than 1/2. The probability of the value on the green die being higher than the value on the blue die is greater than 1/2. The probability of the value on the yellow die being higher than the value on the green die is greater than 1/2. There are definitely a multitude of possible solutions, so I encourage you to attempt to find one using only numbers 1-6 before scrolling down. Got a solution? Let's take a look at the following dice: Yellow : {1, 4, 4, 4, 4, 4} Blue : {2, 2, 2, 5, 5, 5} Green : {3, 3, 3, 3, 3, 6} I should note that my solution is set up to have no ties, which makes the analysis a bit more straightforward. It is certainly possible to come up with interesting solutions which allow ties. 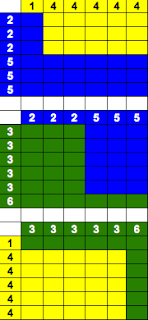The chart on the right shows how each die compares to the others. The color of each square indicates the winner when the number of the same row and column are compared. We can see that blue beats yellow 21 out of 36 times, green beats blue 21 out of 36 times, and yellow beats green 25 out of 36 times. So this combination of dice will show the non-transitive effect we were looking for. So I explain this “sorcery” to you, before you try to burn me at the stake for being a witch, and you calm down. Now I tell you that I’d like to try a new game. I select two dice of the same color, then you get to select two dice of the same color, then we roll both pairs 100 times. The winner this time is the person who rolls a higher total, the sum of their two dice, more times in 100 rolls. I select two yellow dice. After learning of my trick, you decide to pick two blues and proceed to lose 60 out of 100 times. You declare, “‘tis but a statistical error, let’s have another go!” I select two blues and you, two greens. I win again! Just to rub it in, I choose green and you choose yellow, and I win once again. Softly weeping, you listen as I explain that the probabilities have now switched! The chart on the right shows the different sums that are possible for a given set of colored dice. When you look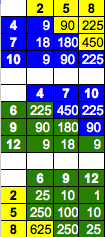 at the possible sum 4 for the blue dice, you see that 4 can meet up with 2 a total of nine times, with blue winning each, 4 can meet up with 5 a total of 90 times with yellow winning each, and can meet up with 8 a total of 225 times with yellow winning each. So the value in each cell is the number of times each match-up can occur, with the color of the cell showing who will win each match-up. There are 6^4 = 1296 possibilities, so winning half corresponds to 648. This dice trick is an example of non-transitive logic, which can certainly be a non-intuitive topic (Stay tuned for some non-transitive logic involving coins!). In this case, you must break your intuition that there must be one “best” die. In science, it’s a great idea to try to look for other examples of the behavior you are observing to help reinforce what you’ve learned. It turns out that one of the most basic schoolyard games involves non-transitive logic! In the game of rock, paper, scissors, we find that rock crushes scissors, scissors cuts paper, and paper covers rock. This is analogous to the behavior of our special dice, and I believe makes the logic much easier to understand. Compare against your intuition, break down and analyze, build up and reinforce.