The bearded half of Hulse-Taylor

A few weeks ago I was on a bus going through Scranton and I read a super-awesome fun fact regarding the Hulse-Taylor binary pulsar in Black Holes, White Dwarfs and Neutron Stars. Sadly, I have since forgotten it and left the book a few thousand miles away. So, let's just make up our own! First, we need a little background. What the heck is a pulsar? A pulsar is a rapidly rotating neutron star that beams electromagnetic radiation towards us, which is how we can see them. Typical rotation periods range from a millisecond to a few seconds. So each time the pulsar rotates, we observe a blip when the radiation beams towards us. Since these objects are additionally very stable rotators, they are essentially very accurate clocks with which we may make astronomical measurements. So what's the Hulse-Taylor binary pulsar? The Hulse-Taylor binary is almost exactly what it sounds like: it's a pulsar binary where one of the pulsars is pointed towards earth. It was the first binary of it's kind discovered and offers a unique look into a very high gravity environment. It also provided a very nice test for General Relativity. General Relativity predicts that two orbiting massive bodies should emit gravitational waves. This emission of gravitational waves will then cause the orbit to decay and the two bodies to move closer together. So does the Hulse-Taylor binary show this? Take a look: 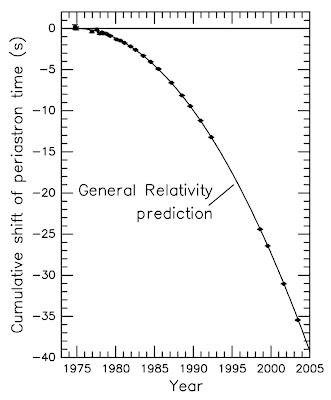The data fit the prediction of general relativity perfectly! For this discovery Hulse and Taylor shared the 1993 Nobel prize in Physics. Now that's all well and good, but I was promised some fun facts...? Ah, yes! Well, we mentioned that the Hulse-Taylor binary orbit is decaying. It turns out that the orbit is decaying at about 3.5 meters per year. That's pretty slow. Let's put it into a more conventional speed, like meters per second. So $$ 3.5 m/yr = 3.5 m/yr \times \frac{1 year}{3.14 \times 10^7 s} = 1.1 \times 10^{-7} m/s $$ or, in less useful units, $$ 3.5 m/yr = 110 nm/s $$ Great, so what to compare this to? Well, all people who are in the know know that I am a manly man who gained the ability to grow facial hair sometime after my sophomore year of college. And since I have to pretend to be an upstanding member of society this week, I happen to know the last time I shaved. Thus, a few simple measurements and I can estimate how long hair takes to grow. The last time I shaved was three days ago and a quick eyeball measurement (sadly I have no ruler) gives a facial hair length of about 2mm. Thus, a beard grows at about 0.7 mm/ day. $$ 0.7 mm/day = 0.7 mm/day \times \frac{10^{-3} m}{mm} \times \frac{1 day}{86400s} = 8 nm/s $$ This is a universal speed constant, which we shall call the speed of beard. Or, bowing to our oppressive overload sponsors, we shall call it "Gillette Mach 1." So doing a quick division, we find that the rate at which the Hulse-Taylor binary's orbit is shrinking is roughly 14 times beard speed, or in our commercial units, Gillette Mach 14 (a razor close shave!). "Well," I hear you cry (a bit disappointed...?), "that's a pretty useless unit, but can't we be more useless?" Yes, dear reader, we certainly can! We are currently at Snuggielevels of uselessness right now, but I think we can just about bump it up to Member of Congress* useless if we try. A furlong is a unit of length about 200 meters long. A fortnight is a unit of time about 14 days long. Therefore, if we want a speed we just... $$ \frac{furlong}{fortnight} = 1 \frac{furlong}{fortnight} \times \frac{200 m}{furlong} \times \frac{1 fortnight}{14 \times 86400 s} = 1.6 \times 10^{-4} \frac{m}{s} $$ So the rate of decay of the Hulse-Taylor binary is: $$ 3.5 \frac{m}{yr} = 1.1 \times 10^{-7} m/s \times \frac{1 furlong/fortnight}{ 1.6 \times 10^{-4} m/s} = 7 \times 10^{-4} \frac{furlong}{fortnight} $$ Hooray! So now we know the decay rate of the Hulse-Taylor binary orbit in two horrible units: either 700 microfurlongs per fortnight or 14 times the speed of beard (AKA Gillette Mach 14). Please write these in your copybooks now and forever commit them to memory. * In no way is The Virtuosi affiliated with the wonderful Gillette Company, which makes the world's best razors. Since we aren't affiliated with this great Gillette company, we are not obligated to repeat their slogan that it's "The Best A Man Can Get" despite its self-evident truth. Nor is the author required to say that the silky smooth shave I get with a Mach 20 razor is the only reason I can even must social interaction. Hooray!

Comments