Sorry for the delay between posts. Here in Virtuosi-land, we've all
begun our summer research projects and I think we've just become a
little bogged down in the rush that is starting a summer research
project. You feel as though you have no idea what the heck is going on,
and just try desperately to keep your head up as you hit the ground
running, but thats a topic for another post. In this post I'd like to
address a fun physics problem.
How long can you balance a pencil on its tip? I mean in a perfect
world, how long?
No really. Think about it a second. Try and come up with an answer
before your proceed. What this question will become by the end of this
post is something like the following:
Given that Quantum Mechanics exists, what is the longest time you
could conceivably balance a pencil, even in principle?
I will walk you through my approach to answering this question. I think
it is a good problem to illustrate how to solve non-trivial physics
problems. I will try and go into some detail about how I arrived at my
solution. For most of you this will probably be quite boring, so feel
free to skip ahead to the last section for some numbers and plots.
Finding an Equation of Motion
The first thing we need to do is find an equation of motion to describe
our system. Lets consider the angle theta that the pencil makes with
respect to the vertical. Lets treat this as a torque problem. Dealing
with rotating systems is almost identical to dealing with free particles
in Newtonian mechanics. Instead of Netwon's first law, relating forces
to acceleration $$ F = m \ddot x $$ we just replace it with the
rotational analogue of force - torque, the rotational analogue of
acceleration - rotational acceleration, and the rotational analogue of
mass - the moment of inertia. $$ T = I \ddot \theta $$ (I've taken the
usual physics notation here, dots represent time derivatives) We need to
determine the torque and moment of inertia of our pencil. At this point
I need to model the system. I need to break up the real world, rather
complicated idea of a pencil, and turn it into an approximation that
retains all of the important bits but enables me to actually proceed.
So, I will model a pencil as a rod, a uniform rod with a constant mass
density. In doing so, I can proceed. The moment of inertia of a rod
about its end is rather easy to calculate. If you are not familiar with
the result I recommend you try the integral yourself. $$ I = \int r^2
\ dm = \frac{1}{3} m l^2 $$\ where m is the total mass of my pencil
and l is its length. I will take a pencil's mass to be 5 g and its
length to be 10 cm. Now the torque. The only force the pencil feels is
the force due to gravity, which acts from the center of mass, which for
my model of a pencil occurs at half its length. I additionally wish to
express the force in terms of the parameter I decided would be useful,
namely theta, the angle the pencil makes with the vertical. I obtain $$
T = r \times F = \frac{1}{2} m g l \sin \theta $$ Great, putting the
pieces together we obtain an equation of motion for our pencil $$
\frac{1}{2} m g l \sin \theta = \frac{1}{3} m l^2 \ddot \theta $$
rearranging I get this into a nicer form $$ \ddot \theta -
\frac{3}{2} \frac{g}{l} \sin \theta = 0 $$ in fact, I'll utilize
another time honored physics trick of the trade and simplify my
expression further by making up a new symbol. Since I've done these
kinds of problems before I can make a rather intelligent replacement $$
\omega^2 = \frac{3}{2} \frac{g}{l} $$ obtaining finally $$ \ddot
\theta - \omega^2 \sin \theta = 0 $$ And we've done it.
Looking at the equation of motion
Now that we've found the equation of motion, lets look at it a bit.
First off, what does an equation of motion tell us? Well, it tells us
all of the physics of our system of interest. That little equation
contains all of the information about how our little model pencil can
move. (Notice that while I haven't yet been explicit about it, in my
model of the pencil, I also don't allow the tip to move at all, the
pencil is only able to pivot about its tip). Great. A useful thing to do
when confronting a new equation of motion is to try and find its fixed
points. I.e. try and find states in which your system can be which do
not evolve in time. How can I do that? Sounds complicated. In fact, I'll
sort of work backwards. I want to know the values that do not evolve in
time, meaning of course that if I were to find such a solution, all of
the terms that depend on time would be zero. So, if such a solution
exists, for that solution the derivative term will vanish. So the
solutions have to be solutions to the much simpler equation $$ \sin
\theta = 0 $$ Which we know the solutions. In fact, lets be a little
smart about things and only worry about theta = 0 and theta = pi.
Thinking back to our model this suggest a pencil being straight up
(theta = 0) and straight down (theta = pi). These are the stable points
of the equation. The second one you are familiar with. If you instead of
balancing a pencil 'up', try to balance it 'down', you know that if you
start with the pencil pointing straight down it stays that way and
doesn't do anything interesting. But what about that first solution
theta =0? That indicates that if you could start this model pencil
exactly straight up, it would stay that way forever, and also not do
anything interesting. Oh no you cry. It seems as though we've already
answered the question. How long can you balance a pencil? It looks like
you could do it forever if you did it perfectly. But you and I both know
that is impossible. You can't ever balance a pencil forever. I've never
done it, and tonight I've spent a lot of time trying. So what went
wrong?
When your approximations fail
So what went wrong again? It seems like I've gotten an answer, namely in
my model you could, at least in principle balance your pencil forever.
But you and I both know you can't. Something is amiss. Hopefully, the
first thought that occurs to you is something along the lines of the
following.
Of course you dummy! You could in principle balance a pencil
forever, but in the real world, you can't set the pencil up standing
perfectly straight. Even if its tilted just a little bit, its going to
fall. This is exactly the problem with your physicists, you don't live
in the real world!
Whoa, lets not be so harsh there. I made some rather crude
approximations in order to get such a simple equation. You are allowed
to make approximations provided (1) they are still right to as many
digits as you care about, and (2) you keep in mind the approximations
you made, and think a bit about how they could go wrong. So, before we
do anything too drastic, lets do with your gut. I agree, it seems like
if the pencil would be at any small angle, it ought to fall. Lets double
check that our equation does that. So for the moment imagine theta being
some small number. In fact, I will use the usual notation and call it
epsilon. What does our equation say then? $$ \ddot \theta = \omega^2
\sin \epsilon $$ lets make another approximation (I know I know, we've
already run into trouble, but bear with me). If epsilon is going to be a
really small number, then we can simplify this equation even more. That
sine being in there is really bugging me. Sines are hard. So lets fix
it. Can we say something about how sine behaves when the angles are
super small?? In fact we can. Such an approach is super common in
physics.
A short side comment on Taylor Series
Imagine a function. Any function. Picture the graph of the function.
I.e. imagine a line on a graph. No matter what function you imagine, if
you zoom in far enough, at any point that function ought to look like a
line. Seriously. Zoom out a little bit and it will look like a line plus
a parabola. Zoom out a little more and it will look like a cubic
polynomial. You can make these statements precise, and thats the Taylor
Expansion. But the idea
isn't much more complicated than what I've described. Taylor expanding
the sine, we obtain $$ \ddot \theta \approx \omega^2 \left(
\epsilon - \frac{\epsilon^3}{3!} + \cdots \right) $$ So if you are
at really small angles, sin(x) looks just like x. Whats really small?
Well as long as x^3 is too small for you to care about. For me, for the
rest of the problem that will be for angles that are less than about 0.1
radians, for which that second term is about 0.00017 radians or 0.01
degrees, which is too small for me to care.
Coming back to the approximation bit
Anywho, for really small angles, our equation of motion is approximately
$$ \ddot \theta = \omega^2 \theta $$ So, notice for a second that
if theta is positive, since omega^2 has to be positive, then our
angular acceleration is going to be positive. So your intuition was
right. If your pencil ever gets to any positive angle, even the smallest
of angles, then our angular acceleration is positive and our pencil will
start to fall down. So. The next question becomes. How can we capture
this bit of reality. It looks like my model has this unphysical
solution. How can I make it more real worldy? Ah, this is the real fun
of physics. You could go in any number of directions. Perhaps you could
try and estimate how good you can actually prepare the angle of the
pencil, perhaps you could ask whether air bouncing into the pencil would
make it fall, perhaps you could wonder whether adding more realism to
the moment of inertia would make the pencil fall easier, maybe you could
wonder whether the thermal motion of the pencil would make it fall?
Maybe you could consider the pencil as an elastic object and consider it
vibrating as well as pivoting. Maybe you could model the tip as being
able to move? Maybe you could introduce the gravitational pull of the
sun? or the moon? or you? or the nearest mountain? The sky's the limit.
So what am I going to do? Quantum Mechanics. Seriously, bear with me a
bit.
A little preliminaries
Before proceeding any further, lets actually solve the equation of
motion we just got for the smallest angles. To remind you, the equation
I got for my model of a pencil in the limit of the smallest angles was
$$ \ddot \theta = \omega^2 \theta $$ This is an equation I can
solve. Its a very common differential equation, and one that we use and
abuse in physics so I know the solution by heart. So lets write it down.
First just to let know you, this sort of equation, second derivative of
thing being linearly proportional to thing gives you solutions that are
always pairs, usually, depending on the sign of the constant, they are
written as sines and cosines, or decaying and growing exponentials.
Naturally of course in order to solve a second order differential
equation, we need to specify two initial conditions. In this case I will
call them theta_0 and dot theta_0, representing the initial position
and initial angular velocity. In this form the solution can actually
most easily be written in terms of the exponential pair associated with
sine and cosine, sinh and cosh (you can read more about them
here, they are really neat
functions). The solution is $$ \theta(t) = \theta_0 \cosh \omega t
+ \dot \theta_0 /\omega \sinh \omega t $$ which as you could
probably convince yourself, exponentially grows for any positive
theta_0 or dot theta_0.
Abandoning Realism
At this point of considering the question, I turned down a different
route. I don't really care about balancing pencils on my desk. You see,
I know a curious fact. I know that in quantum mechanics there is an
uncertainty principle which says that you cannot precisely know both the
position and momentum of an object. This of course means that even in
principle, since our world is dominated by quantum mechanics, I could
never actually balance even my model pencil forever, because I could
never prepare it with perfect initial conditions. The uncertainly
principle tells us
that the best possible resolution I could have in the position and
momentum of an object are set by Planck's constant: $$ \Delta x \Delta
p \geq \frac{\hbar}{2} $$ This has to be true for our pencil as well.
In fact I can translate the uncertainty principle into its angular form
$$ \Delta \theta \Delta J \geq \frac{\hbar }{2} $$ where theta is
our theta and J is the angular momentum, which for our pencil we know is
$$ J = I \dot \theta = \frac{1}{3} m l^2 $$ So the uncertainty
principle for our pencil is, $$ \Delta \theta \Delta \dot \theta
\geq \frac{3 \hbar }{2 m l^2 } \approx 3.2 \times 10^{-30}
\text{ Hz} $$ So what? So, I'm going to approximate the effects the
uncertainty relation has on our pencil problem by saying that when I
start off the classical mechanical pencil, I'm going to require that my
initial conditions satisfy the uncertainty relation: $$ \theta_0
\dot\theta_0 = \frac{3 \hbar }{2 ml^2} $$ which we decided is
going to mean that our pencil has to fall. The real question is? How
long will it take this pseudo-quantum mechanical pencil to fall? In
order words the question I am really trying to answer is:
Assuming a completly rigid pencil which you place in a vaccum and cool
down to a few millikelvin so that it is in its ground state. Roughly
how long will it take this pencil to fall?
Do it to it
So lets do it. This is going to be a bit quick, mostly because its
getting late and I want to go to bed. But the procedure is kind of
straight forward now. I need to choose initial conditions subject to the
above constraint, figure out how long a pencil with those initial
conditions takes to get to theta = pi/2 (i.e. fall over), and then do it
over and over again for different values of the initial conditions. So,
the first thing to do is figure out how to pick initial conditions that
satisfy the constraint. I'll do this systematically by parameterizing
the problem in terms of the ratio of the initial conditions. I.e. lets
define $$ \log_{10} \frac{\theta_0}{\dot \theta_0} = R $$ where
I've taken the log for convenience. Now, figuring how long the pencil
takes to fall in principle is just numerically integrating forward the
full equation of motion $$ \ddot \theta = \omega^2 \sin \theta $$
where I need to do it numerically because the sine makes this equation
too hard to solve analytically. In order to do the numerical integration
I implemented a Runge-Kutta
algorithm in python. The only problem is that I am dealing with really
small numbers and my algorithm can't play well with those in any
reasonable amount of time. But, I can solve analytically for the
equations of motion in the small angle limit, so I actually use the
solution $$ \theta(t) = \theta_0 \cosh \omega t + \dot \theta_0
/ \omega \sinh \omega t $$ to evolve the system up to an angle of 0.1
radians, and then let the nonlinear equation and runge kutta algorithm
take over. The full python code for my problem is available
here
(if you want to run it, remove the .txt extension, I did that so that it
would be previewable). And what do I obtain? First looking over 20
orders of magnitude in differential initial conditions:
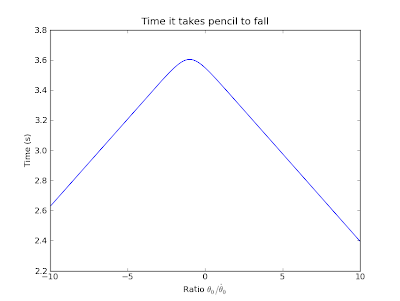
And second, zooming into the interesting region.
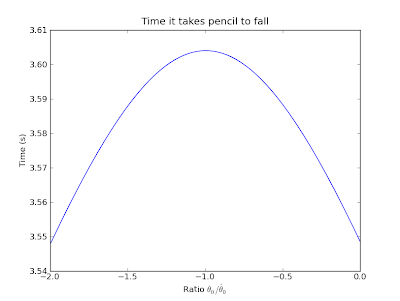
So, what is the best time you could balance a quantum mechanical pencil,
i.e. what is the absolute longest time you could hope to balance a
pencil in our universe? About 3.5 seconds. Seriously. Think about that
for a second. Usually you hear about the uncertainty principle, and it
seems like a neat parlor trick, but something that couldn't influence
your day to day lives, and here is a remarkable problem where even in
the best case, the uncertainty principle puts a hard limit on
championship pencil balancing which seems tantalizingly close. And there
you have a graduate student working through a somewhat non trivial
problem. I probably went into way too much details with the basics, but
we are still trying to feel out who our audience is. Please leave
comments and let me know if I either could have left things out, or
should have went into more details at parts.
EDIT
As per request, here is how the max fall time scales with the length of
the pencil assuming a pencil with uniform density.
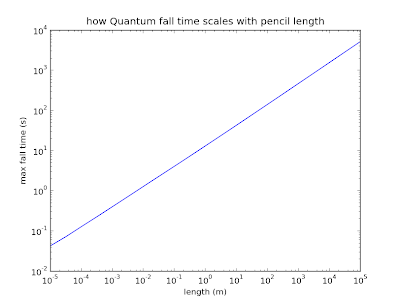
Plotted on a log-log plot, that is a pretty darn good line. The power
law dependence is $$ t \sim l^{0.514} $$ Neat. Strangely enough, if I
trust my numbers here, the longest you could hope to balance a 'pencil'
1 km long would be about 6 minutes. Thats a very strange mental picture.