Falling Ice

It's been a while since I posted anything, much to my shame. Hopefully this post marks a change in that streak. Today I'm going to consider a very practical application of all this physics stuff. One of my housemates parks his car on the side of the house, with the front of the car facing the house. Living in Ithaca, NY, the weather has been the usual cold and snowy, like the rest of the northeast USA this winter. Yet, early last week, we had some unusually warm weather, in the 30s (fahrenheit). A few days later, my housemate went out to his car, and discovered that falling chunks of ice had broken his windshield! Now, to be clear here, I'm not talking about icicles, I'm talking about large, block-like, chunks. My best guess is that during the warm days, snow on the roof turned into chunks of ice, and slid off the roof. The question I'm going to try to answer today is: How far from the house could these chunks possibly land? Put another way, what I want to know is, how far from the house would we have to park our cars to not risk broken windshields from falling ice? The First Attempt We'll start with the simplest assumptions we can think of. First, we'll assume that there is no friction on the ice block as it slides down the roof. We'll also assume there's no air resistance slowing down the ice in the air. The maximum range will be given by a block of ice sliding from the top of the roof. Taking the height of the peak of the roof as h, relative to the edge of the roof, we can write down the magnitude of the velocity of the ice chunk when it reaches the edge of the roof. We start by setting the change in gravitational potential energy equal to the change in kinetic energy. Recalling the form for both of these, $$PE=mgh$$ $$KE=\tfrac{1}{2}mv^2$$ we can set these equal and solve for v, $$mgh = \tfrac{1}{2}mv^2$$ so $$|v|=\sqrt{2gh}$$ This should be a familiar expression to anyone who went through introductory mechanics. Now, given that the roof is at an angle theta, we can write down the x (horizontal) and y (vertical) components of velocity, $$v_x=|v|\cos\theta$$ $$v_y=-|v|\sin \theta$$ where I've introduced a minus sign in the y component of velocity to indicate that the ice chunk is falling. Now that we have the velocity, we have to call upon some more kinematics. To figure out how far the ice flies, we have to know how long it is in the air. So we start by considering the vertical motion. The distance traveled by an object with an initial velocity, v_0, and a constant acceleration, a, is given by $$\Delta y=\tfrac{1}{2}at^2+v_0t$$ In our case, the distance traveled is the height of the first two floors of my house. The acceleration is that of gravity, g, and the initial velocity is the y component of velocity we found above. We'd like to find the time it takes to travel this distance. We have to be a little careful with our minus signs, by our convention the acceleration is in the negative direction, and the change in position is negative. Working all of that out, and plugging in our known values, we get $$\tfrac{1}{2}gt^2+|v|\sin \theta t - l =0$$ where l is the height of the house. We can solve this for t, finding $$t=\frac{-|v|\sin \theta + \sqrt{(|v|\sin \theta)^2+2gl}}{g}$$ The horizontal distance traveled is simply the horizontal velocity times the time, $$x=\frac{|v|\cos\theta}{g}(-|v|\sin \theta + \sqrt{(|v|\sin \theta)^2+2gl})$$ a result that you may recognize as the 'projectile range formula' (particularly if I brought the minus on the v sine theta term into the sine, indicating that I'm firing at a negative angle, that is, downwards). Having found that result, lets plug in our velocity, and then some numbers. First, $$x=\frac{\sqrt{2gh}\cos\theta}{g}(\sqrt{2gh}\sin \theta + \sqrt{(2gh\sin^2 \theta+2gl})$$ Now, for some estimation. I'd say that the height of the roof peak is 10 ft, the height of the first two floors of the house is 20 ft, and the angle of the roof is 30 degrees. Having made those estimates, now I just have to plug in all the numbers, yielding $$x=5.2 m=17 ft$$ That's a very long range! Now, I didn't see any chunks of ice that were more than about 7 ft from the house. So we have to question what went wrong with the above derivation. Well, maybe nothing went wrong. I did calculate the maximum range. It's quite possible none of these ice chunks were from the very top of the roof. Still, I'm inclined to think we may have overestimated. I'd say that our initial velocity was too high. The ice, as it comes down the roof, will have to push a bunch of snow out of the way. Even though it may not have much friction with the roof, all that snow will slow it down, and reduce the velocity with which it comes off. I'm just going to guess that about half of the potential energy it had is lost to the snow and roof, as a rough estimation. That would give a velocity $$|v| = \sqrt{gh}$$ and a maximum distance of $$x= 4m = 13ft$$ which is closer to what I observed. The Second Attempt I'm still not completely satisfied with the previous work, the answer doesn't match my observation. As a wise man (Einstein) once said, "make things as simple as possible, but no simpler." I may be guilty of making the problem too simple here. So I'm going to add back in air resistance. In general, we physicists like to avoid this because it usually means we can't get nice, analytic expressions as answers (like the one I have above). Instead, we usually just have to calculate the result numerically. This isn't the end of the world, and often times it is actually a bit easier, but it's not as pretty looking. Still, to satisfy myself, and you, gentle reader, I will step into that realm. We start by writing down the force on our block of ice once it is falling. We've got gravity, and air resistance. Thus $$\vec{F}=-mg\hat{y}-bv^2\hat{v}$$ I've input a drag force that goes as v^2, and is in the opposite direction of v. The 'v direction' is a cop out, because I didn't want to do the explicit direction, so lets fix that. We'll have x and y components, and we note that the magnitude of v times the direction of v is the velocity vector. So, $$\vec{F}=-mg\hat{y}-bv\hat{v}_x-bv\hat{v}_y$$ Breaking this up into components we get $$a_x=-\frac{bv}{m}v_x$$ $$a_y=-g-\frac{bv}{m}v_y$$ This is as far as we can take this work analytically. I'll say a little more about the coefficient b. This depends on the exact size and shape of the object, as well as the medium it is moving through. I'm going to use $$b=.4\rho A$$ because that's what we used for hay bales in my classical mechanics class years ago. Here, rho is the density of air, and A is the surface area of the object. I would estimate that the large face of the ice chunk is roughly one square foot, or .1 m^2. I'd estimate the mass of the ice was around 2 kg. Now, for some magic. I've put all of this into mathematica, and asked it to solve this numerically. First we have the plot for the full initial velocity, $$v=\sqrt{2gh}$$

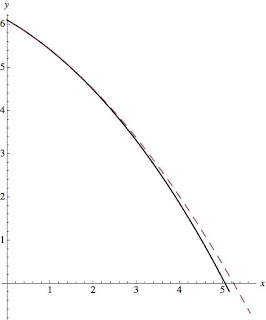The solid line is with air resistance, the dashed line without air resistance. The plot shows vertical vs. horizontal distance, and the units are meters. (click to enlarge)

Next we have the plot for the half initial velocity, $$v=\sqrt{gh}$$

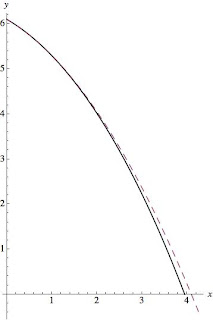The solid line is with air resistance, the dashed line without air resistance. The plot shows vertical vs. horizontal distance, and the units are meters. (click to enlarge)

As you can see from the plots, in neither case does it make a large difference, about .2 m. The Third Round The final thought that occurs to me is that perhaps I got the angle of the roof wrong. That would be quite easy. Humans are notoriously bad at estimating angles. I'll plot the results (with air resistance) for 15, 30, and 45 degree angles and the lower velocity.

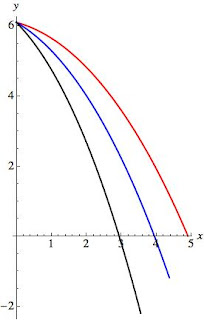The plot shows vertical vs. horizontal distance, and the units are meters. The red line is 15 degrees, the blue line is 30 degrees, and the black line is 45 degrees. (click to enlarge)

In summary, the answer is unclear. What I really need to do is measure the angle of my roof better, because there's a significant angle dependence. It's also quite possible that we didn't see a maximum distance hit (thankfully!). In addition, air resistance doesn't seem to matter much in this particular problem, probably because the distance the thing falls is short enough that terminal velocity is not reached. Hopefully this gave you a bit of a taste of a more practical physics problem, and how to approach air resistance (if you want to see the mathematica code, let me know). The lesson here seems to be either don't park too close to roofs, or have insurance for your windshield!