Remember when you first learned about other planets and their many fun facts? You were probably bombarded by such truisms as: "Jupiter is approximately the mass of 318 Earths, has a orbital period that is 4,300 Earth days, is made out of pure love, and is mostly transparent." Well, I was curious about what Clicky's day was like in terms of Earth days. When did Clicky get to sleep, when did he eat dinner, what is his orbital radius and eccentricity? To do this, I looked at only the 3rd column of the data that you may or may not have downloaded yesterday from here. Starting out, it should be noted that this is not an ordinary time series where you have some value measured at given intervals. It is actually a series of time points at which a click was entered. I thought it would be most natural to go ahead and bins these to give a sense of the access to Clicky over the past two months. It looks something like this: 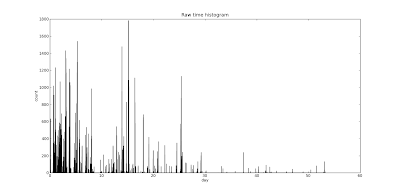Well, that wasn't as informative as I had hoped. We see some spikes here and there with a general trend toward neglect and abandonment towards the end of the second month. What if we take these days and bin them into one single day worth of traffic? We get this: 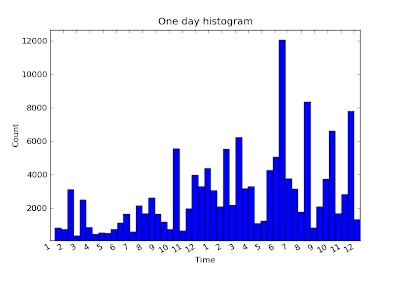Again, not so informative yet, but we are definitely starting to see some structure in the day. In particular, there is a lot of activity in the afternoon and evening with a definite lull around 5pm. There is also a distinct minima around 5am. It appears that Clicky is on the average most active between noon and 9pm, getting a break through most of the night. Next, let's look at the autocorrelation of the times. For standard time series, the autocorrelation is defined to be $$ C_{ss}(\tau) = \int_{-\infty}^{\infty}s(t) * \bar s(t-\tau) dt $$ which measures the amount of similarity in a signal as a function of the time separation between two points. Again, we don't have a continuous signal, so our autocorrelation function is instead a histogram of the all-pairs differences in the data points that we do have. That is, start at the first time point and subtract it from all of the other time points in the series. Then, move to the next data point and subtract it from all the subsequent times while keeping tracking of all of these differences. This is our autocorrelation in real space. 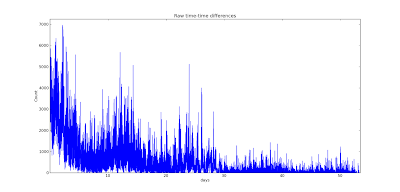We can also zoom in and smooth the data a bit 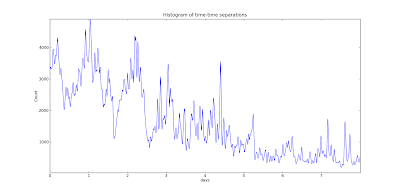Ah, now there we go. We see a distinct over-abundance of time differences around 1 day, 2 days, etc. What is the primary oscillation we see in the correlation? To see that, let's look at the frequency space autocorrelation and plot its power, or square. 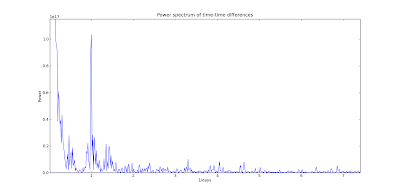Finally, we get the primary component of the variation of Clicky's visits throughout the 2 month period that he was in operation. It occurs, to within error, at 1 day. No very surprising at all. I'm sure we could look more closely at the peak and its width, but I am satisfied to say that Clicky's day is defined by the Earth day to within a few percent. *In response to more messages in Clicky, we agree that it is "So slow." Rest assured, management is looking into the problem.

Comments